Introduction
Overview
Teaching: 40 min
Exercises: 15 minQuestions
What is Deep Learning?
When does it make sense to use and not use Deep Learning?
When is it successful?
What are the tools involved?
What is the workflow for Deep Learning?
Why did we choose to use Keras in this lesson?
Objectives
Recall the sort of problems for which Deep Learning is a useful tool
List some of the available tools for Deep Learning
Recall the steps of a Deep Learning workflow
Identify the inputs and outputs of a deep neural network.
Explain the operations performed in a single neuron
Test that you have correctly installed the Keras, Seaborn and Sklearn libraries
What is Deep Learning?
Deep Learning, Machine Learning and Artificial Intelligence
Deep Learning (DL) is just one of many techniques collectively known as machine learning. Machine learning (ML) refers to techniques where a computer can “learn” patterns in data, usually by being shown numerous examples to train it. People often talk about machine learning being a form of Artificial Intelligence (AI). Definitions of artificial intelligence vary, but usually involve having computers mimic the behaviour of intelligent biological systems. Since the 1950s many works of science fiction have dealt with the idea of an artificial intelligence which matches (or exceeds) human intelligence in all areas. Although there have been great advances in AI and ML research recently we can only come close to human like intelligence in a few specialist areas and are still a long way from a general purpose AI. The image below shows some differences between artificial intelligence, Machine Learning and Deep Learning.
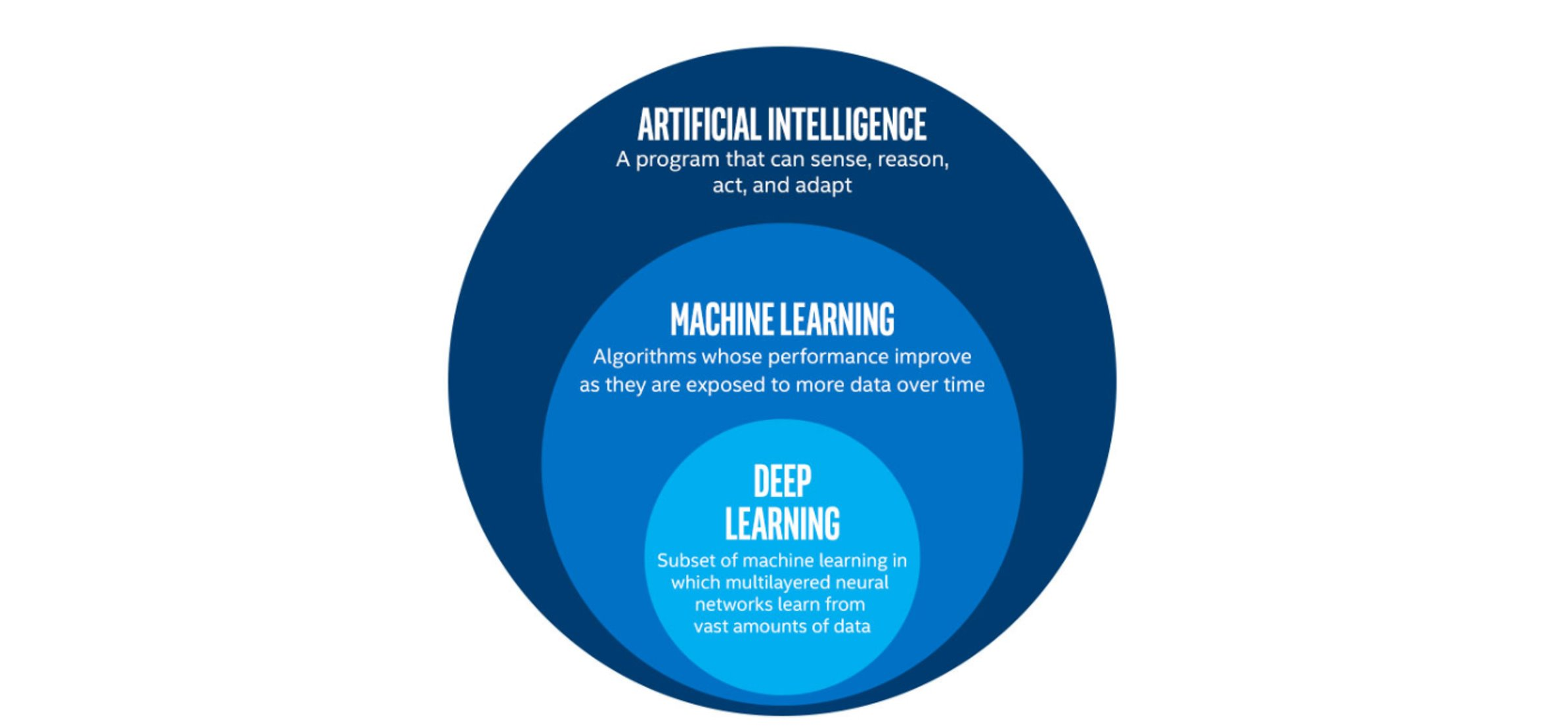 The image above is by Tukijaaliwa, CC BY-SA 4.0, via Wikimedia Commons, original source
The image above is by Tukijaaliwa, CC BY-SA 4.0, via Wikimedia Commons, original source
Neural Networks
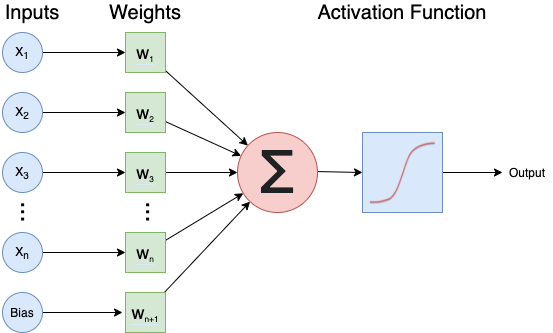
A neural network is an artificial intelligence technique loosely based on the way neurons in the brain work. A neural network consists of connected computational units called neurons. Each neuron …
- has one or more inputs, e.g. input data expressed as floating point numbers
- most of the time, each neuron conducts 3 main operations:
- take the weighted sum of the inputs
- add an extra constant weight (i.e. a bias term) to this weighted sum
- apply a non-linear function to the output so far (using a predefined activation function)
- return one output value, again a floating point number
Multiple neurons can be joined together by connecting the output of one to the input of another. These connections are associated with weights that determine the ‘strength’ of the connection, the weights are adjusted during training. In this way, the combination of neurons and connections describe a computational graph, an example can be seen in the image below. In most neural networks neurons are aggregated into layers. Signals travel from the input layer to the output layer, possibly through one or more intermediate layers called hidden layers. The image below shows an example of a neural network with three layers, each circle is a neuron, each line is an edge and the arrows indicate the direction data moves in.
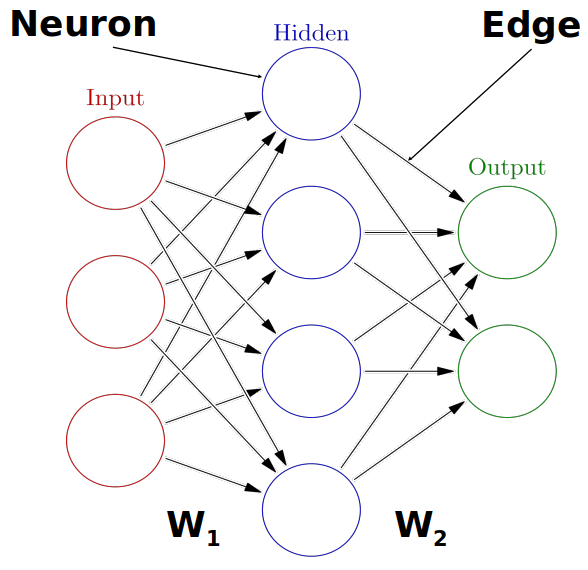 The image above is by Glosser.ca, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons, original source
The image above is by Glosser.ca, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons, original source
Calculate the output for one neuron
Suppose we have
- Input: X = (0, 0.5, 1)
- Weights: W = (-1, -0.5, 0.5)
- Bias: b = 1
- Activation function relu:
f(x) = max(x, 0)What is the output of the neuron?
Note: You can use whatever you like: brain only, pen&paper, Python, Excel…
Solution
Weighted sum of input: 0 * (-1) + 0.5 * (-0.5) + 1 * 0.5 = 0.25
Add the bias: 0.25 + 1 = 1.25
Apply activation function: max(1.25, 0) = 1.25
So, neuron output = 1.25
Neural networks aren’t a new technique, they have been around since the late 1940s. But until around 2010 neural networks tended to be quite small, consisting of only 10s or perhaps 100s of neurons. This limited them to only solving quite basic problems. Around 2010 improvements in computing power and the algorithms for training the networks made much larger and more powerful networks practical. These are known as deep neural networks or Deep Learning.
Deep Learning requires extensive training using example data which shows the network what output it should produce for a given input. One common application of Deep Learning is classifying images. Here the network will be trained by being “shown” a series of images and told what they contain. Once the network is trained it should be able to take another image and correctly classify its contents. But we are not restricted to just using images, any kind of data can be learned by a Deep Learning neural network. This makes them able to appear to learn a set of complex rules only by being shown what the inputs and outputs of those rules are instead of being taught the actual rules. Using these approaches Deep Learning networks have been taught to play video games and even drive cars. The data on which networks are trained usually has to be quite extensive, typically including thousands of examples. For this reason they are not suited to all applications and should be considered just one of many machine learning techniques which are available.
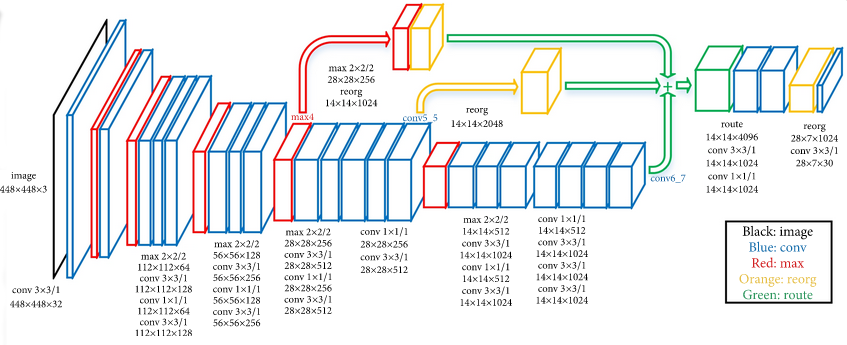
While traditional “shallow” networks might have had between three and five layers, deep networks often have tens or even hundreds of layers. This leads to them having millions of individual weights. The image below shows a diagram of all the layers (there are too many neurons to draw them all) on a Deep Learning network designed to detect pedestrians in images. The input (left most) layer of the network is an image and the final (right most) layer of the network outputs a zero or one to determine if the input data belongs to the class of data we are interested in. This image is from the paper “An Efficient Pedestrian Detection Method Based on YOLOv2” by Zhongmin Liu, Zhicai Chen, Zhanming Li, and Wenjin Hu published in Mathematical Problems in Engineering, Volume 2018
What sort of problems can Deep Learning solve?
- Pattern/object recognition
- Segmenting images (or any data)
- Translating between one set of data and another, for example natural language translation.
- Generating new data that looks similar to the training data, often used to create synthetic datasets, art or even “deepfake” videos.
- This can also be used to give the illusion of enhancing data, for example making images look sharper, video look smoother or adding colour to black and white images. But beware of this, it is not an accurate recreation of the original data, but a recreation based on something statistically similar, effectively a digital imagination of what that data could look like.
Examples of Deep Learning in Research
Here are just a few examples of how Deep Learning has been applied to some research problems. Note: some of these articles might be behind paywalls.
- Detecting COVID-19 in chest X-ray images
- Forecasting building energy load
- Protein function prediction
- Simulating Chemical Processes
- Help to restore ancient murals
What sort of problems can Deep Learning not solve?
- Any case where only a small amount of training data is available.
- Tasks requiring an explanation of how the answer was arrived at.
- Classifying things which are nothing like their training data.
What sort of problems can Deep Learning solve, but should not be used for?
Deep Learning needs a lot of computational power, for this reason it often relies on specialised hardware like graphical processing units (GPUs). Many computational problems can be solved using less intensive techniques, but could still technically be solved with Deep Learning.
The following could technically be achieved using Deep Learning, but it would probably be a very wasteful way to do it:
- Logic operations, such as computing totals, averages, ranges etc. (see this example applying Deep Learning to solve the “FizzBuzz” problem often used for programming interviews)
- Modelling well defined systems, where the equations governing them are known and understood.
- Basic computer vision tasks such as edge detection, decreasing colour depth or blurring an image.
Deep Learning Problems Exercise
Which of the following would you apply Deep Learning to?
- Recognising whether or not a picture contains a bird.
- Calculating the median and interquartile range of a dataset.
- Identifying MRI images of a rare disease when only one or two example images available for training.
- Identifying people in pictures after being trained only on cats and dogs.
- Translating English into French.
Solution
- and 5 are the sort of tasks often solved with Deep Learning.
- is technically possible but solving this with Deep Learning would be extremely wasteful, you could do the same with much less computing power using traditional techniques.
- will probably fail because there is not enough training data.
- will fail because the Deep Learning system only knows what cats and dogs look like, it might accidentally classify the people as cats or dogs.
How much data do you need for Deep Learning?
The rise of Deep Learning is partially due to the increased availability of very large datasets. But how much data do you actually need to train a Deep Learning model? Unfortunately, this question is not easy to answer. It depends, among other things, on the complexity of the task (which you often do not know beforehand), the quality of the available dataset and the complexity of the network. For complex tasks with large neural networks, we often see that adding more data continues to improve performance. However, this is also not a generic truth: if the data you add is too similar to the data you already have, it will not give much new information to the neural network.
In case you have too little data available to train a complex network from scratch, it is sometimes possible to use a pretrained network that was trained on a similar problem. Another trick is data augmentation, where you expand the dataset with artificial data points that could be real. An example of this is mirroring images when trying to classify cats and dogs. An horizontally mirrored animal retains the label, but exposes a different view.
Deep Learning workflow
To apply Deep Learning to a problem there are several steps we need to go through:
1. Formulate/ Outline the problem
Firstly we must decide what it is we want our Deep Learning system to do. Is it going to classify some data into one of a few categories? For example if we have an image of some hand written characters, the neural network could classify which character it is being shown. Or is it going to perform a prediction? For example trying to predict what the price of something will be tomorrow given some historical data on pricing and current trends.
2. Identify inputs and outputs
Next we need to identify what the inputs and outputs of the neural network will be. This might require looking at our data and deciding what features of the data we can use as inputs. If the data is images then the inputs could be the individual pixels of the images.
For the outputs we will need to look at what we want to identify from the data. If we are performing a classification problem then typically we will have one output for each potential class.
3. Prepare data
Many datasets are not ready for immediate use in a neural network and will require some preparation. Neural networks can only really deal with numerical data, so any non-numerical data (for example words) will have to be somehow converted to numerical data.
Next we will need to divide the data into multiple sets. One of these will be used by the training process and we will call it the training set. Another will be used to evaluate the accuracy of the training and we will call that one the test set. Sometimes we will also use a 3rd set known as a validation set to tune hyperparameters.
4. Choose a pre-trained model or build a new architecture from scratch
Often we can use an existing neural network instead of designing one from scratch. Training a network can take a lot of time and computational resources. There are a number of well publicised networks which have been shown to perform well at certain tasks, if you know of one which already does a similar task well then it makes sense to use one of these.
If instead we decide we do want to design our own network then we need to think about how many input neurons it will have, how many hidden layers and how many outputs, what types of layers we use (we will explore the different types later on). This will probably need some experimentation and we might have to try tweaking the network design a few times before we see acceptable results.
5. Choose a loss function and optimizer
The loss function tells the training algorithm how far away the predicted value was from the true value. We will look at choosing a loss function in more detail later on.
The optimizer is responsible for taking the output of the loss function and then applying some changes to the weights within the network. It is through this process that the “learning” (adjustment of the weights) is achieved.
6. Train the model
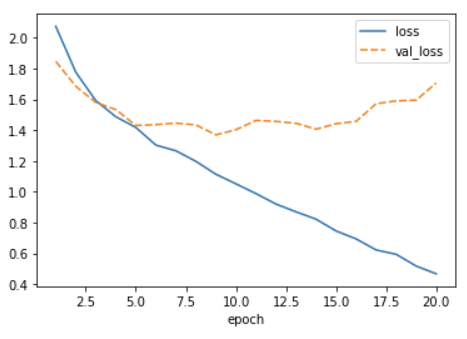
We can now go ahead and start training our neural network. We will probably keep doing this for a given number of iterations through our training dataset (referred to as epochs) or until the loss function gives a value under a certain threshold. The graph below show the loss against the number of epochs, generally the loss will go down with each epoch, but occasionally it will see a small rise.
7. Perform a Prediction/Classification
After training the network we can use it to perform predictions. This is the mode you would use the network in after you have fully trained it to a satisfactory performance. Doing predictions on a special hold-out set is used in the next step to measure the performance of the network.
8. Measure Performance
Once we trained the network we want to measure its performance. To do this we use some additional data that was not part of the training, this is known as a test set. There are many different methods available for measuring performance and which one is best depends on the type of task we are attempting. These metrics are often published as an indication of how well our network performs.
9. Tune Hyperparameters
Hyperparameters are all the parameters set by the person configuring the machine learning instead of those learned by the algorithm itself. The hyperparameters include the number of epochs or the parameters for the optimizer. It might be necessary to adjust these and re-run the training many times before we are happy with the result.
10. Share Model
Now that we have a trained network that performs at a level we are happy with we can go and use it on real data to perform a prediction. At this point we might want to consider publishing a file with both the architecture of our network and the weights which it has learned (assuming we did not use a pre-trained network). This will allow others to use it as as pre-trained network for their own purposes and for them to (mostly) reproduce our result.
Deep Learning workflow exercise
Think about a problem you would like to use Deep Learning to solve.
- What do you want a Deep Learning system to be able to tell you?
- What data inputs and outputs will you have?
- Do you think you will need to train the network or will a pre-trained network be suitable?
- What data do you have to train with? What preparation will your data need? Consider both the data you are going to predict/classify from and the data you will use to train the network.
Discuss your answers with the group or the person next to you.
Deep Learning Libraries
There are many software libraries available for Deep Learning including:
TensorFlow
TensorFlow was developed by Google and is one of the older Deep Learning libraries, ported across many languages since it was first released to the public in 2015. It is very versatile and capable of much more than Deep Learning but as a result it often takes a lot more lines of code to write Deep Learning operations in TensorFlow than in other libraries. It offers (almost) seamless integration with GPU accelerators and Google’s own TPU (Tensor Processing Unit) chips that are built specially for machine learning.
PyTorch
PyTorch was developed by Facebook in 2016 and is a popular choice for Deep Learning applications. It was developed for Python from the start and feels a lot more “pythonic” than TensorFlow. Like TensorFlow it was designed to do more than just Deep Learning and offers some very low level interfaces. PyTorch Lightning offers a higher level interface to PyTorch to set up experiments. Like TensorFlow it is also very easy to integrate PyTorch with a GPU. In many benchmarks it outperforms the other libraries.
Keras
Keras is designed to be easy to use and usually requires fewer lines of code than other libraries. We have chosen it for this workshop for that reason. Keras can actually work on top of TensorFlow (and several other libraries), hiding away the complexities of TensorFlow while still allowing you to make use of their features.
The performance of Keras is sometimes not as good as other libraries and if you are going to move on to create very large networks using very large datasets then you might want to consider one of the other libraries. But for many applications the performance difference will not be enough to worry about and the time you will save with simpler code will exceed what you will save by having the code run a little faster.
Keras also benefits from a very good set of online documentation and a large user community. You will find that most of the concepts from Keras translate very well across to the other libraries if you wish to learn them at a later date.
Installing Keras and other dependencies
Follow the instructions in the setup document to install Keras, Seaborn and Sklearn.
Testing Keras Installation
Lets check you have a suitable version of Keras installed. Open up a new Jupyter notebook or interactive python console and run the following commands:
from tensorflow import keras print(keras.__version__)Solution
You should get a version number reported. At the time of writing 2.4.0 is the latest version.
2.4.0
Testing Seaborn Installation
Lets check you have a suitable version of seaborn installed. In your Jupyter notebook or interactive python console run the following commands:
import seaborn print(seaborn.__version__)Solution
You should get a version number reported. At the time of writing 0.11.1 is the latest version.
0.11.1
Testing Sklearn Installation
Lets check you have a suitable version of sklearn installed. In your Jupyter notebook or interactive python console run the following commands:
import sklearn print(sklearn.__version__)Solution
You should get a version number reported. At the time of writing 0.24.1 is the latest version.
0.24.1
Key Points
Machine learning is the process where computers learn to recognise patterns of data.
Artificial neural networks are a machine learning technique based on a model inspired by groups of neurons in the brain.
Artificial neural networks can be trained on example data.
Deep Learning is a machine learning technique based on using many artificial neurons arranged in layers.
Deep Learning is well suited to classification and prediction problems such as image recognition.
To use Deep Learning effectively we need to go through a workflow of: defining the problem, identifying inputs and outputs, preparing data, choosing the type of network, choosing a loss function, training the model, tuning Hyperparameters, measuring performance before we can classify data.
Keras is a Deep Learning library that is easier to use than many of the alternatives such as TensorFlow and PyTorch.
Classification by a Neural Network using Keras
Overview
Teaching: 30-60 min
Exercises: 40-45 minQuestions
What is a neural network?
How do I compose a Neural Network using Keras?
How do I train this network on a dataset?
How do I get insight into learning process?
How do I measure the performance of the network?
Objectives
Use the deep learning workflow to structure the notebook
Explore the dataset using pandas and seaborn
Use one-hot encoding to prepare data for classification in Keras
Describe a fully connected layer
Implement a fully connected layer with Keras
Use Keras to train a small fully connected network on prepared data
Interpret the loss curve of the training process
Use a confusion matrix to measure the trained networks’ performance on a test set
Introduction
In this episode we will learn how to create and train a Neural Network using Keras to solve a simple classification task.
The goal of this episode is to quickly get your hands dirty (no.. not from fieldwork) in actually defining and training a neural network, without going into depth of how neural networks work on a technical or mathematical level. We want you to go through the most commonly used deep learning workflow that was covered in the introduction. As a reminder below are the steps of the deep learning workflow:
- Formulate / Outline the problem
- Identify inputs and outputs
- Prepare data
- Choose a pretrained model or start building architecture from scratch
- Choose a loss function and optimizer
- Train the model
- Perform a Prediction/Classification
- Measure performance
- Tune hyperparameters
- Save model
In this episode we will focus on a minimal example for each of these steps, later episodes will build on this knowledge to go into greater depth for some or all of these steps.
GPU usage
For this lesson having a GPU (graphics card) available is not needed. We specifically use very small toy problems so that you do not need one. However, Keras will use your GPU automatically when it is available. Using a GPU becomes necessary when tackling larger datasets or complex problems which require a more complex Neural Network.
1. Formulate/outline the problem: classification
In this episode we will be using a subset of the below the surface dataset of which the original dataset can be downloaded as csv file here.
Data processing
To make the dataset suitable for an English Audience the column names have been translated from Dutch. Furthermore
Furthermore, the various fields in the dataset have been assessed ans classified in the following criteria:
- Adminstrative (e.g. find number, projectnumber, archaeological unit etc.)
- Measurement (length, weight, diameter etc. )
- Characteristic (characteristics of the object which does not necessaryly be done by an expert, like color or type of blade, decoration technique)
- Interpretation (Classification by an expert preferably to a reference collection / typochronology)
The classification was done on this file from the project and based on doman knowledge by Maurice de Kleijn. The result of this assessment can be found here.
Note that the distinction between Characteristic and Interpretation is a bit arbitrary
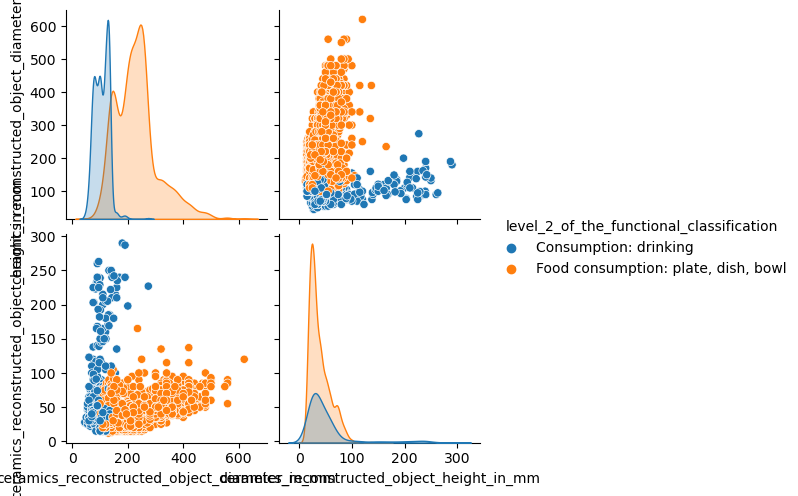
For this workshop we decided to look at ceramics. Since the aim is to automatically categorize data based on a variety of characteristics we decided to look at ceramics and see if we can train a neural network that distinguishes ceramics that are cateogorized as “plate, dish, bowl” from ceramics that are categorized as “drinking” based on non interpreted measurements on the dimensions (i.e. height and width), surface treatment and type of material. We thus try to see if the experts could be replaced by our neural nework. Please note, that we have simplified the question and that we the aim of this analysis is purely educational.
The subest has been created based on the a python script, which can be accessed here
The subset that the script created can ben accessed here). Please make sure to download this one (the other links are just a reference).
We will use this dataset to train a neural network which can classify the second level of the functional classification ( of the archeological artefect, based on certain features.
Goal
The goal is to predict the second level of functional classification using the attributes available in this dataset.
2. Identify inputs and outputs
To identify the inputs and outputs that we will use to design the neural network we need to familiarize ourselves with the dataset. This step is sometimes also called data exploration.
We will start by importing the pandas library that will help us read the dataset from the .csv file. Pandas is a fast, powerful, flexible and easy to use open source data analysis and manipulation tool, built on top of the Python programming language.
import pandas as pd
We can load the dataset using
ds = pd.read_csv('data/subset_ceramics_v30032023.csv')
This will give you a pandas dataframe which contains the data.
Inspect Dataset
Inspect the dataset.
- What are the different features called in the dataframe?
- Are the target classes of the dataset stored as numbers or strings?
- How many samples does this dataset have?
- How many NaN (Not a Number) are there for each feature? Tip: Use pandas functions: head describe unique isna sum
Solution
1. Using the pandas
headfunction you can see the names of the features. Using thedescribefunction we can also see some statistics for the numeric columnsds.head()ds.describe()2. We can get the unique values in the
l2_classcolumn using theuniquefunction of pandas. It shows the target class is stored as a string and has 3 unique values. This type of column is usually called a ‘categorical’ column.ds["l2_class"].unique()array(['Food consumption: plate, dish, bowl', 'Consumption: drinking', 'Food preparation: cooking - and hearth utensils', 'Food preparation and consumption: various parts of kitchenware', 'Consumption of tobacco and stimulants', 'Consumption of food and drinks: table accessories', 'Food consumption: cutlery and tools'], dtype=object)3. Using
describefunction on this column shows there are 3410 samples with 7 unique classifications.ds["l2_class"].describe()count 3410 unique 7 top Food consumption: plate, dish, bowl freq 2144 Name: l2_class, dtype: object4. Using a combination of
isnaandsumfunction on the dataset shows that some columns have a lot of NaNs.ds.isna().sum()find_number 0 material 0 start_date 0 end_date 0 l2_class 0 object_diameter 0 object_height 0 ceramics_image_type 2413 ceramics_mark 3308 on_website 0 material_simplified 0 url 2652 dtype: int64
Input and Output Selection
Now that we have familiarized ourselves with the dataset we can select the data attributes to use as input for the neural network and the target that we want to predict.
Choice of Input and Output
Inspect the dataset and identify suitable input features and output
Solution
A few possible comments:
- Columns
object_diameterandobject_heightcan be good features.- Columns
ceramics_image_typeandceramics_markfor example are not good features due to very high number of NaNs.- Columns
start_dateandend_dateare do not make good features as they are not related to the classification we want to achieve.
In the rest of this episode we will use the object_diameter, object_height, material_simplified attributes.
The target for the classification task will be the l2_class.
Data Exploration
Exploring the data is an important step to familiarize yourself with the problem and to help you determine the relevant inputs and outputs.
3. Prepare data
Remove unnecessary columns of data
The dataset currently contains a lot of redundant or unnecessary data columns. We will remove all columns except our input and output columns.
ds_preprocessed = ds[['l2_class', 'object_diameter', 'object_height', 'material_simplified']]
The input data and target data are not yet in a format that is suitable to use for training a neural network.
Clean missing values
During the exploration phase we saw that some rows in the dataset have missing (NaN)
values, leaving such values in the input data will ruin the training, so we need to deal with them.
There are many ways to deal with missing values, but for now we will just remove the offending rows by adding a call to dropna():
# Drop the rows that have NaN values in them
ds_preprocessed = ds_preprocessed.dropna()
Simplify output
Let’s explore the output classification column by looking at the number of data rows for each unique classification using the value_counts pandas function.
ds_preprocessed['l2_class'].value_counts()
Food consumption: plate, dish, bowl 2144
Consumption: drinking 874
Food preparation: cooking - and hearth utensils 255
Food preparation and consumption: various parts of kitchenware 107
Consumption of food and drinks: table accessories 24
Consumption of tobacco and stimulants 4
Food consumption: cutlery and tools 2
Name: l2_class, dtype: int64
There are two categories with notable data points in Food consumption: plate, dish, bowl and Consumption: drinking. We will focus on these for our neural network. To remove the others we will query the pandas dataframe.
ds_preprocessed = ds_preprocessed.query("l2_class == ['Consumption: drinking', 'Food consumption: plate, dish, bowl']")
Change output type if needed
The output column is our categorical target, however pandas still sees it as the
generic type Object. We can convert this to the pandas categorical type:
ds_preprocessed['l2_class'] = ds_preprocessed['l2_class'].astype('category')
This will make later interaction with this column a little easier.
Pairplot: Visual Aid
Looking at numbers on a screen usually does not give a very good intuition about the data we are working with. So let us use a visualization tool called Pairplot which is useful for datasets with relatively few attributes. This can be created using
sns.pairplot(...)which can be imported from the seaborn package. It shows a scatterplot of each attribute plotted against each of the other attributes.import seaborn as sns sns.pairplot(ds_preprocessed, hue = 'l2_class')
Prepare target data for training
Second, the target data is also in a format that cannot be used in training.
A neural network can only take numerical inputs and outputs, and learns by
calculating how “far away” the species predicted by the neural network is
from the true species.
When the target is a string category column as we have here it is very difficult to determine this “distance” or error.
Therefore we will transform this column into a more suitable format.
Again there are many ways to do this, however we will be using the one-hot encoding.
This encoding creates multiple columns, as many as there are unique values, and
puts a 1 in the column with the corresponding correct class, and 0’s in
the other columns.
For instance, for a classification of the Consumption: drinking type, the one-hot encoding would be 0 1
Fortunately pandas is able to generate this encoding for us.
target = pd.get_dummies(ds_preprocessed['l2_class'])
target.head() # print out the top 5 to see what it looks like.
Prepare input data for training
Similar to the target column l2_class, we also have the material_simplified feature column which is a string and needs to be one-hot encoded. Let us first look at the unique values in the column.
ds_preprocessed['material_simplified'].unique()
Let us now convert the string input in to a categorical input and perform the one-hot encoding of the results.
ds_preprocessed['material_categorized'] = ds_preprocessed['material_simplified'].astype('category')
ds_features = pd.get_dummies(ds_preprocessed['material_categorized'])
Let us now combine all the features to create one input feature dataset
ds_features = ds_features.join(ds_preprocessed.drop(columns=['l2_class', 'material_simplified', 'material_categorized']))
One-hot encoding vs ordinal encoding
- How many output neurons will our network have now that we one-hot encoded the target class?
- Another encoding method is ‘ordinal encoding’. Here the variable is represented by a single column, where each category is represented by a different integer (0, 1 in this case). How many output neurons will a network have when ordinal encoding is used?
Solution
- 2, one for each output variable class
- 1, the 2 classes are represented in a single variable
Split data into training and test set
Finally, we will split the dataset into a training set and a test set. As the names imply we will use the training set to train the neural network, while the test set is kept separate. We will use the test set to assess the performance of the trained neural network on unseen samples. In many cases a validation set is also kept separate from the training and test sets (i.e. the dataset is split into 3 parts). This validation set is then used to select the values of the parameters of the neural network and the training methods. For this episode we will keep it at just a training and test set however.
To split the cleaned dataset into a training and test set we will use a very convenient
function from sklearn called train_test_split.
The output of the function are:
- the input features of the dataset for training (
X_train) and testing (X_test) and the corresponding training targets (y_train) and test targets (y_test).
This function takes a number of input parameters:
- The first two are the dataset (i.e. features) and the corresponding targets.
- Next is the named parameter
test_sizethis is the fraction of the dataset that is used for testing, in this case0.2means 20% of the data will be used for testing. random_statecontrols the shuffling of the dataset, setting this value will reproduce the same results (assuming you give the same integer) every time it is called.shufflewhich can be eitherTrueorFalse, it controls whether the order of the rows of the dataset is shuffled before splitting. It defaults toTrue. Note that it shuffles the rows but keeps the integrity of each row.stratifyis a more advanced parameter that controls how the split is done. By setting it totargetthe train and test sets the function will return will have roughly the same proportions (with regards to the number of second level classification) as the dataset.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(ds_features, target,test_size=0.2, random_state=0, shuffle=True, stratify=target)
Training and Test sets
Take a look at the training and test set we created.
- How many samples do the training and test sets have?
- Are the classes in the training set well balanced?
Solution
Using
y_train.shapeandy_test.shapewe can see the training set has 273 samples and y_test has 69 samples.We can check the balance of classes by counting the number of ones for each of the columns in the one-hot-encoded target, which shows the training set has 699 data points for
Consumption: drinking, and 1715 forFood consumption: plate, dish, bowl.y_train.sum()Consumption: drinking 699 Food consumption: plate, dish, bowl 1715 dtype: int64The dataset is not perfectly balanced, but it is not orders of magnitude out of balance either. So we will leave it as it is.
4. Build an architecture from scratch or choose a pretrained model
Keras for neural networks
For this lesson we will be using Keras to define and train our neural network
models.
Keras is a machine learning framework with ease of use as one of its main features.
It is part of the tensorflow python package and can be imported using from tensorflow import keras.
Keras includes functions, classes and definitions to define deep learning models, cost functions and optimizers (optimizers are used to train a model).
Before we move on to the next section of the workflow we need to make sure we have Keras imported. We do this as follows:
from tensorflow import keras
For this class it is useful if everyone gets the same results from their training. Keras uses a random number generator at certain points during its execution. Therefore we will need to set two random seeds, one for numpy and one for tensorflow:
from numpy.random import seed
seed(1)
from tensorflow.random import set_seed
set_seed(2)
Build a neural network from scratch
We will now build out first neural network from scratch. Although this sounds like a daunting task, you will experience that with Keras it is actually surprisingly straightforward.
With Keras you compose a neural network by creating layers and linking them
together. For now we will only use one type of layer called a fully connected
or Dense layer. In Keras this is defined by the keras.layers.Dense class.
A dense layer has a number of neurons, which is a parameter you can choose when you create the layer. When connecting the layer to its input and output layers every neuron in the dense layer gets an edge (i.e. connection) to all of the input neurons and all of the output neurons. The hidden layer in the image in the introduction of this episode is a Dense layer.
The input in Keras also gets special treatment, Keras automatically calculates the number of inputs
and outputs a layer needs and therefore how many edges need to be created.
This means we need to let Keras now how big our input is going to be.
We do this by instantiating a keras.Input class and tell it how big our input is.
inputs = keras.Input(shape=X_train.shape[1])
We store a reference to this input class in a variable so we can pass it to the creation of our hidden layer. Creating the hidden layer can then be done as follows:
hidden_layer = keras.layers.Dense(10, activation="relu")(inputs)
The instantiation here has 2 parameters and a seemingly strange combination of parentheses, so
let us take a closer look.
The first parameter 10 is the number of neurons we want in this layer, this is one of the
hyperparameters of our system and needs to be chosen carefully. We will get back to this in the section
on hyperparameter tuning.
The second parameter is the activation function to use, here we choose relu which is 0
for inputs that are 0 and below and the identity function (returning the same value)
for inputs above 0.
This is a commonly used activation function in deep neural networks that is proven to work well.
Next we see an extra set of parenthenses with inputs in them, this means that after creating an
instance of the Dense layer we call it as if it was a function.
This tells the Dense layer to connect the layer passed as a parameter, in this case the inputs.
Finally we store a reference so we can pass it to the output layer in a minute.
Now we create another layer that will be our output layer. Again we use a Dense layer and so the call is very similar to the previous one.
output_layer = keras.layers.Dense(2, activation="softmax")(hidden_layer)
Because we chose the one-hot encoding, we use 2 neurons for the output layer.
The softmax activation ensures that the two output neurons produce values in the range (0, 1) and they sum to 1. We can interpret this as a kind of ‘probability’ that the sample belongs to a certain species.
Now that we have defined the layers of our neural network we can combine them into a Keras model which facilitates training the network.
model = keras.Model(inputs=inputs, outputs=output_layer)
model.summary()
The model summary here can show you some information about the neural network we have defined.
Create the neural network
With the code snippets above, we defined a Keras model with 1 hidden layer with 10 neurons and an output layer with 2 neurons.
- How many parameters does the resulting model have?
- What happens to the number of parameters if we increase or decrease the number of neurons in the hidden layer?
Solution
inputs = keras.Input(shape=X_train.shape[1]) hidden_layer = keras.layers.Dense(10, activation="relu")(inputs) output_layer = keras.layers.Dense(2, activation="softmax")(hidden_layer) model = keras.Model(inputs=inputs, outputs=output_layer) model.summary()Model: "model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) [(None, 10)] 0 _________________________________________________________________ dense (Dense) (None, 10) 110 _________________________________________________________________ dense_1 (Dense) (None, 2) 22 ================================================================= Total params: 132 Trainable params: 132 Non-trainable params: 0 _________________________________________________________________The model has 132 trainable parameters. If you increase the number of neurons in the hidden layer the number of trainable parameters in both the hidden and output layer increases or decreases accordingly of neurons. The name in quotes within the string
Model: "model"may be different in your view; this detail is not important.
How to choose an architecture?
Even for this small neural network, we had to make a choice on the number of hidden neurons. Other choices to be made are the number of layers and type of layers (as we will see later). You might wonder how you should make these architectural choices. Unfortunately, there are no clear rules to follow here, and it often boils down to a lot of trial and error. However, it is recommended to look what others have done with similar datasets and problems. Another best practice is to start with a relatively simple architecture. Once running start to add layers and tweak the network to see if performance increases.
Choose a pretrained model
If your data and problem is very similar to what others have done, you can often use a pretrained network. Even if your problem is different, but the data type is common (for example images), you can use a pretrained network and finetune it for your problem. A large number of openly available pretrained networks can be found in the Model Zoo, pytorch hub or tensorflow hub.
5. Choose a loss function and optimizer
We have now designed a neural network that in theory we should be able to train to classify our archeological finds. However, we first need to select an appropriate loss function that we will use during training. This loss function tells the training algorithm how wrong, or how ‘far away’ from the true value the predicted value is.
For the one-hot encoding that we selected before a fitting loss function is the Categorical Crossentropy loss.
In Keras this is implemented in the keras.losses.CategoricalCrossentropy class.
This loss function works well in combination with the softmax activation function
we chose earlier.
The Categorical Crossentropy works by comparing the probabilities that the
neural network predicts with ‘true’ probabilities that we generated using the one-hot encoding.
This is a measure for how close the distribution of the two neural network outputs corresponds to the distribution of the two values in the one-hot encoding.
It is lower if the distributions are more similar.
For more information on the available loss functions in Keras you can check the documentation.
Next we need to choose which optimizer to use and, if this optimizer has parameters, what values to use for those. Furthermore, we need to specify how many times to show the training samples to the optimizer.
Once more, Keras gives us plenty of choices all of which have their own pros and cons, but for now let us go with the widely used Adam optimizer. Adam has a number of parameters, but the default values work well for most problems. So we will use it with its default parameters.
Combining this with the loss function we decided on earlier we can now compile the
model using model.compile.
Compiling the model prepares it to start the training.
model.compile(optimizer='adam', loss=keras.losses.CategoricalCrossentropy())
6. Train model
We are now ready to train the model.
Training the model is done using the fit method, it takes the input data and
target data as inputs and it has several other parameters for certain options
of the training.
Here we only set a different number of epochs.
One training epoch means that every sample in the training data has been shown
to the neural network and used to update its parameters.
history = model.fit(X_train, y_train, epochs=100)
The fit method returns a history object that has a history attribute with the training loss and potentially other metrics per training epoch. It can be very insightful to plot the training loss to see how the training progresses. Using seaborn we can do this as follow:
sns.lineplot(x=history.epoch, y=history.history['loss'])
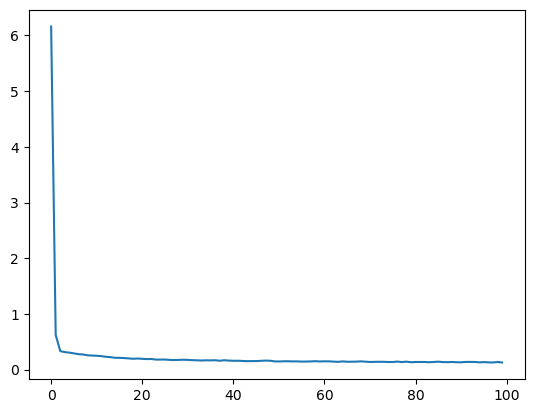
This plot can be used to identify whether the training is well configured or whether there are problems that need to be addressed.
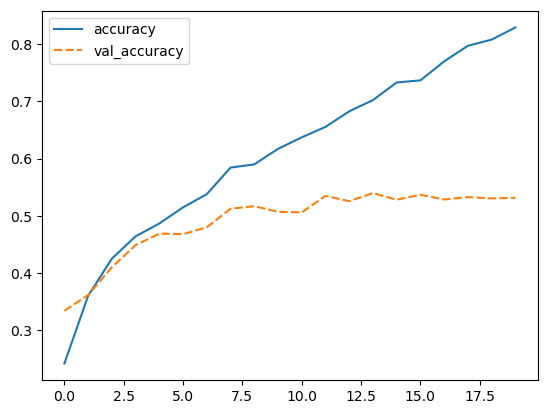
The Training Curve
Looking at the training curve we have just made.
- How does the training progress?
- Does the training loss increase or decrease?
- Does it change fast or slowly?
- Is the graph look very jittery?
- Do you think the resulting trained network will work well on the test set?
Solution
- The loss curve should drop quite quickly in a smooth line with little jitter
- The results of the training give very little information on its performance on a test set. You should be careful not to use it as an indication of a well trained network.
7. Perform a prediction/classification
Now that we have a trained neural network, we can use it to predict new samples using the predict function.
We will use the neural network to predict the second level classification of the test set
using the predict function.
We will be using this prediction in the next step to measure the performance of our
trained network.
This will return a numpy matrix, which we convert
to a pandas dataframe to easily see the labels.
y_pred = model.predict(X_test)
prediction = pd.DataFrame(y_pred, columns=target.columns)
prediction
Output
Consumption: drinking Food consumption: plate, dish, bowl 0 1.192648e-18 9.999999e-01 1 2.878897e-04 9.997121e-01 2 9.933218e-01 6.678253e-03 3 1.550273e-11 9.999999e-01 4 9.999999e-01 1.860956e-36 ... ... ... 599 4.948534e-01 5.051466e-01 600 1.249560e-04 9.998751e-01 601 1.192672e-03 9.988073e-01 602 9.193144e-01 8.068555e-02 603 1.893464e-01 8.106536e-01 604 rows × 2 columns
Remember that the output of the network uses the softmax activation function and has two
outputs, one for each classification. This dataframe shows this nicely.
We now need to transform this output to one classification type per sample.
We can do this by looking for the index of highest valued output and converting that
to the corresponding classification.
Pandas dataframes have the idxmax function, which will do exactly that.
predicted_class = prediction.idxmax(axis="columns")
predicted_class
Output
0 Food consumption: plate, dish, bowl 1 Food consumption: plate, dish, bowl 2 Consumption: drinking 3 Food consumption: plate, dish, bowl 4 Consumption: drinking ... 599 Food consumption: plate, dish, bowl 600 Food consumption: plate, dish, bowl 601 Food consumption: plate, dish, bowl 602 Consumption: drinking 603 Food consumption: plate, dish, bowl Length: 604, dtype: object
8. Measuring performance
Now that we have a trained neural network it is important to assess how well it performs. We want to know how well it will perform in a realistic prediction scenario, measuring performance will also come back when tuning the hyperparameters.
We have created a test set during the data preparation stage X_test and y_test, which we will use now to create a confusion matrix.
Confusion matrix
With the predicted classification we can now create a confusion matrix and display it
using seaborn.
To create a confusion matrix we will use another convenient function from sklearn
called confusion_matrix.
This function takes as a first parameter the true labels of the test set.
We can get these by using the idxmax method on the y_test dataframe.
The second parameter is the predicted labels which we did above.
from sklearn.metrics import confusion_matrix
true_class = y_test.idxmax(axis="columns")
matrix = confusion_matrix(true_class, predicted_class)
print(matrix)
[[169 6]
[ 7 422]]
Unfortunately, this matrix is kinda hard to read. Its not clear which column and which row corresponds to which class. So let’s convert it to a pandas dataframe with its index and columns set to the classes as follows:
# Convert to a pandas dataframe
confusion_df = pd.DataFrame(matrix, index=y_test.columns.values, columns=y_test.columns.values)
# Set the names of the x and y axis, this helps with the readability of the heatmap.
confusion_df.index.name = 'True Label'
confusion_df.columns.name = 'Predicted Label'
We can then use the heatmap function from seaborn to create a nice visualization of
the confusion matrix.
The annot=True parameter here will put the numbers from the confusion matrix in
the heatmap.
sns.heatmap(confusion_df, annot=True)
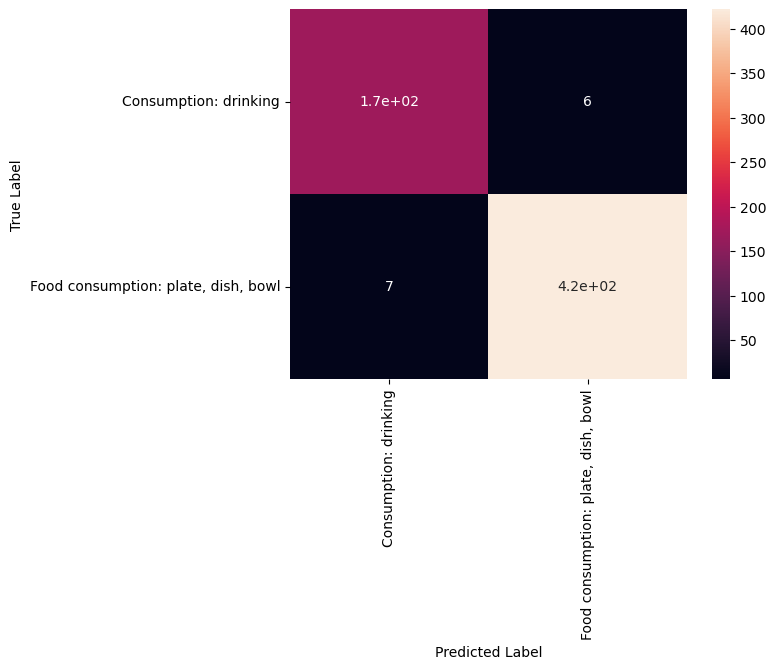
Confusion Matrix
Measure the performance of the neural network you trained and visualize a confusion matrix.
- Did the neural network perform well on the test set?
- Did you expect this from the training loss you saw?
- What could we do to improve the performance?
Solution
The confusion matrix shows that the predictions for the two classes are quite accurate, but could be improved.
The training loss was very low, so from that perspective this may be expected. But always keep in mind that a good training loss does not ensure excellent performance on new data set. That is why a test set is important when training neural networks.
We can try many things to improve the performance from here. One of the first things we can try is to balance the dataset better. Other options include: changing the network architecture or changing the training parameters
9. Tune hyperparameters
As we discussed before the design and training of a neural network comes with many hyper parameter choices. We will go into more depth of these hyperparameters in later episodes. For now it is important to realize that the parameters we chose were somewhat arbitrary and more careful consideration needs to be taken to pick hyperparameter values.
10. Share model
It is very useful to be able to use the trained neural network at a later
stage without having to retrain it.
This can be done by using the save method of the model.
It takes a string as a parameter which is the path of a directory where the model is stored.
model.save('my_first_model')
This saved model can be loaded again by using the load_model method as follows:
pretrained_model = keras.models.load_model('my_first_model')
This loaded model can be used as before to predict.
# use the pretrained model here
y_pretrained_pred = pretrained_model.predict(X_test)
pretrained_prediction = pd.DataFrame(y_pretrained_pred, columns=target.columns.values)
# idxmax will select the column for each row with the highest value
pretrained_predicted_class = pretrained_prediction.idxmax(axis="columns")
print(pretrained_predicted_class)
Key Points
The deep learning workflow is a useful tool to structure your approach, it helps to make sure you do not forget any important steps.
Exploring the data is an important step to familiarize yourself with the problem and to help you determine the relavent inputs and outputs.
One-hot encoding is a preprocessing step to prepare labels for classification in Keras.
A fully connected layer is a layer which has connections to all neurons in the previous and subsequent layers.
keras.layers.Dense is an implementation of a fully connected layer, you can set the number of neurons in the layer and the activation function used.
To train a neural network with Keras we need to first define the network using layers and the Model class. Then we can train it using the model.fit function.
Plotting the loss curve can be used to identify and troubleshoot the training process.
The loss curve on the training set does not provide any information on how well a network performs in a real setting.
Creating a confusion matrix with results from a test set gives better insight into the network’s performance.
Monitor the training process
Overview
Teaching: 135 min
Exercises: 80 minQuestions
How do I create a neural network for a regression task?
How do I monitor the training process?
How do I detect (and avoid) overfitting?
What are common options to improve the model performance?
Objectives
Explain the importance of keeping your test set clean, by validating on the validation set instead of the test set
Use the data splits to plot the training process
Design a neural network for a regression task
Measure the performance of your deep neural network
Interpret the training plots to recognize overfitting
Use normalization as preparation step for Deep Learning
Implement basic strategies to prevent overfitting
In this episode we will explore how to monitor the training progress, evaluate our the model predictions and finetune the model to avoid over-fitting. For that we will use a more complicated weather data-set.
We have considerded to adapt this course for an archaeological audience, however given the fact that it only a one day workshop we have not implemented and tested this. We did make a subset for Metal artefacts, of which our ideas for implementation can be found here, feel free to paly around with it.
1. Formulate / Outline the problem: weather prediction
Here we want to work with the weather prediction dataset (the light version) which can be downloaded from Zenodo. It contains daily weather observations from 11 different European cities or places through the years 2000 to 2010. For all locations the data contains the variables ‘mean temperature’, ‘max temperature’, and ‘min temperature’. In addition, for multiple locations, the following variables are provided: ‘cloud_cover’, ‘wind_speed’, ‘wind_gust’, ‘humidity’, ‘pressure’, ‘global_radiation’, ‘precipitation’, ‘sunshine’, but not all of them are provided for every location. A more extensive description of the dataset including the different physical units is given in accompanying metadata file. The full dataset comprises of 10 years (3654 days) of collected weather data across Europe.
A very common task with weather data is to make a prediction about the weather sometime in the future, say the next day. In this episode, we will try to predict tomorrow’s sunshine hours, a challenging-to-predict feature, using a neural network with the available weather data for one location: BASEL.
2. Identify inputs and outputs
Import Dataset
We will now import and explore the weather data-set:
import pandas as pd
filename_data = "weather_prediction_dataset_light.csv"
data = pd.read_csv(filename_data)
data.head()
| DATE | MONTH | BASEL_cloud_cover | BASEL_humidity | BASEL_pressure | … | |
|---|---|---|---|---|---|---|
| 0 | 20000101 | 1 | 8 | 0.89 | 1.0286 | … |
| 1 | 20000102 | 1 | 8 | 0.87 | 1.0318 | … |
| 2 | 20000103 | 1 | 5 | 0.81 | 1.0314 | … |
| 3 | 20000104 | 1 | 7 | 0.79 | 1.0262 | … |
| 4 | 20000105 | 1 | 5 | 0.90 | 1.0246 | … |
Load the data
If you have not downloaded the data yet, you can also load it directly from Zenodo:
data = pd.read_csv("https://zenodo.org/record/5071376/files/weather_prediction_dataset_light.csv?download=1")
Brief exploration of the data
Let us start with a quick look at the type of features that we find in the data.
data.columns
Index(['DATE', 'MONTH', 'BASEL_cloud_cover', 'BASEL_humidity',
'BASEL_pressure', 'BASEL_global_radiation', 'BASEL_precipitation',
'BASEL_sunshine', 'BASEL_temp_mean', 'BASEL_temp_min', 'BASEL_temp_max',
...
'SONNBLICK_temp_min', 'SONNBLICK_temp_max', 'TOURS_humidity',
'TOURS_pressure', 'TOURS_global_radiation', 'TOURS_precipitation',
'TOURS_temp_mean', 'TOURS_temp_min', 'TOURS_temp_max'],
dtype='object')
Exercise: Explore the dataset
Let’s get a quick idea of the dataset.
- How many data points do we have?
- How many features does the data have (don’t count month and date as a feature)?
- What are the different types of measurements (humidity etc.) in the data and how many are there?
- (Optional) Plot the amount of sunshine hours in Basel over the course of a year. Are there any interesting properties that you notice?
Solution
data.shapeThis will give both the number of datapoints (3654) and the number of features (89 + month + date).
To see what type of features the data contains we could run something like:
import string print({x.lstrip(string.ascii_uppercase + "_") for x in data.columns if x not in ["MONTH", "DATE"]}){'cloud_cover', 'precipitation', 'sunshine', 'global_radiation', 'temp_mean', 'humidity', 'pressure', 'temp_min', 'temp_max'}An alternative way which is slightly more complicated but gives better results is using regex.
import re feature_names = set() for col in data.columns: feature_names.update(re.findall('[^A-Z]{2,}', col)) feature_namesIn total there are 9 different measured variables.
Optional exercise
You can plot the sunshine hours in Basel as follows:
data.iloc[:365]['BASEL_sunshine'].plot(xlabel="Day",ylabel="Basel sunchine hours")
There are a couple of things that might stand out to you. For example, it looks like the sunshine hours are fluctuating a lot per day. There also seems to be seasonal fluctuation, with the peaks becoming higher around the middle of the year.
3. Prepare data
Select a subset and split into data (X) and labels (y)
The full dataset comprises of 10 years (3654 days) from which we will select only the first 3 years. The present dataset is sorted by “DATE”, so for each row i in the table we can pick a corresponding feature and location from row i+1 that we later want to predict with our model. As outlined in step 1, we would like to predict the sunshine hours for the location: BASEL.
nr_rows = 365*3
# data
X_data = data.loc[:nr_rows].drop(columns=['DATE', 'MONTH'])
# labels (sunshine hours the next day)
y_data = data.loc[1:(nr_rows + 1)]["BASEL_sunshine"]
In general, it is important to check if the data contains any unexpected values such as 9999 or NaN or NoneType. You can use the pandas data.describe() or data.isnull() function for this. If so, such values must be removed or replaced.
In the present case the data is luckily well prepared and shouldn’t contain such values, so that this step can be omitted.
Split data and labels into training, validation, and test set
As with classical machine learning techniques, it is required in deep learning to split off a hold-out test set which remains untouched during model training and tuning. It is later used to evaluate the model performance. On top, we will also split off an additional validation set, the reason of which will hopefully become clearer later in this lesson.
To make our lives a bit easier, we employ a trick to create these 3 datasets, training set, test set and validation set, by calling the train_test_split method of scikit-learn twice.
First we create the training set and leave the remainder of 30 % of the data to the two hold-out sets.
from sklearn.model_selection import train_test_split
X_train, X_holdout, y_train, y_holdout = train_test_split(X_data, y_data, test_size=0.3, random_state=0)
Now we split the 30 % of the data in two equal sized parts.
X_val, X_test, y_val, y_test = train_test_split(X_holdout, y_holdout, test_size=0.5, random_state=0)
Setting the random_state to 0 is a short-hand at this point. Note however, that changing this seed of the pseudo-random number generator will also change the composition of your data sets. For the sake of reproducibility, this is one example of a parameters that should not change at all.
4. Choose a pretrained model or start building architecture from scratch
Regression and classification
In episode 2 we trained a dense neural network on a classification task. For this one hot encoding was used together with a Categorical Crossentropy loss function.
This measured how close the distribution of the neural network outputs corresponds to the distribution of the three values in the one hot encoding.
Now we want to work on a regression task, thus not predicting a class label (or integer number) for a datapoint. In regression, we like to predict one (and sometimes many) values of a feature. This is typically a floating point number.
Exercise: Architecture of the network
As we want to design a neural network architecture for a regression task, see if you can first come up with the answers to the following questions:
- What must be the dimension of our input layer?
- We want to output the prediction of a single number. The output layer of the NN hence cannot be the same as for the classification task earlier. This is because the
softmaxactivation being used had a concrete meaning with respect to the class labels which is not needed here. What output layer design would you choose for regression? Hint: A layer withreluactivation, withsigmoidactivation or no activation at all?- (Optional) How would we change the model if we would like to output a prediction of the precipitation in Basel in addition to the sunshine hours?
Solution
- The shape of the input layer has to correspond to the number of features in our data: 89
- The output is a single value per prediction, so the output layer can consist of a dense layer with only one node. The softmax activiation function works well for a classification task, but here we do not want to restrict the possible outcomes to the range of zero and one. In fact, we can omit the activation in the output layer.
- The output layer should have 2 neurons, one for each number that we try to predict. Our y_train (and val and test) then becomes a (n_samples, 2) matrix.
In our example we want to predict the sunshine hours in Basel (or any other place in the dataset) for tomorrow based on the weather data of all 18 locations today. BASEL_sunshine is a floating point value (i.e. float64). The network should hence output a single float value which is why the last layer of our network will only consist of a single node.
We compose a network of two hidden layers to start off with something. We go by a scheme with 100 neurons in the first hidden layer and 50 neurons in the second layer. As activation function we settle on the relu function as a it proved very robust and widely used. To make our live easier later, we wrap the definition of the network in a method called create_nn.
from tensorflow import keras
def create_nn():
# Input layer
inputs = keras.Input(shape=(X_data.shape[1],), name='input')
# Dense layers
layers_dense = keras.layers.Dense(100, 'relu')(inputs)
layers_dense = keras.layers.Dense(50, 'relu')(layers_dense)
# Output layer
outputs = keras.layers.Dense(1)(layers_dense)
return keras.Model(inputs=inputs, outputs=outputs, name="weather_prediction_model")
model = create_nn()
The shape of the input layer has to correspond to the number of features in our data: 89. We use X_data.shape[1] to obtain this value dynamically
The output layer here is a dense layer with only 1 node. And we here have chosen to use no activation function. While we might use softmax for a classification task, here we do not want to restrict the possible outcomes for a start.
In addition, we have here chosen to write the network creation as a function so that we can use it later again to initiate new models.
Let us check how our model looks like by calling the summary method.
model.summary()
Model: "weather_prediction_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input (InputLayer) [(None, 89)] 0
_________________________________________________________________
dense (Dense) (None, 100) 9000
_________________________________________________________________
dense_1 (Dense) (None, 50) 5050
_________________________________________________________________
dense_2 (Dense) (None, 1) 51
=================================================================
Total params: 14,101
Trainable params: 14,101
Non-trainable params: 0
When compiling the model we can define a few very important aspects. We will discuss them now in more detail.
5. Choose a loss function and optimizer
Loss function
The loss is what the neural network will be optimized on during training, so choosing a suitable loss function is crucial for training neural networks.
In the given case we want to stimulate that the predicted values are as close as possible to the true values. This is commonly done by using the mean squared error (mse) or the mean absolute error (mae), both of which should work OK in this case. Often, mse is preferred over mae because it “punishes” large prediction errors more severely.
In Keras this is implemented in the keras.losses.MeanSquaredError class (see Keras documentation: https://keras.io/api/losses/). This can be provided into the model.compile method with the loss parameter and setting it to mse, e.g.
model.compile(loss='mse')
Optimizer
Somewhat coupled to the loss function is the optimizer that we want to use. The optimizer here refers to the algorithm with which the model learns to optimize on the provided loss function. A basic example for such an optimizer would be stochastic gradient descent. For now, we can largely skip this step and pick one of the most common optimizers that works well for most tasks: the Adam optimizer. Similar to activation functions, the choice of optimizer depends on the problem you are trying to solve, your model architecture and your data. Adam is a good starting point though, which is why we chose it.
model.compile(optimizer='adam',
loss='mse')
Metrics
In our first example (episode 2) we plotted the progression of the loss during training.
That is indeed a good first indicator if things are working alright, i.e. if the loss is indeed decreasing as it should with the number of epochs.
However, when models become more complicated then also the loss functions often become less intuitive.
That is why it is good practice to monitor the training process with additional, more intuitive metrics.
They are not used to optimize the model, but are simply recorded during training.
With Keras such additional metrics can be added via metrics=[...] parameter and can contain one or multiple metrics of interest.
Here we could for instance chose to use 'mae' the mean absolute error, or the the root mean squared error (RMSE) which unlike the mse has the same units as the predicted values. For the sake of units, we choose the latter.
model.compile(optimizer='adam',
loss='mse',
metrics=[keras.metrics.RootMeanSquaredError()])
Let’s create a compile_model function to easily compile the model throughout this lesson:
def compile_model(model):
model.compile(optimizer='adam',
loss='mse',
metrics=[keras.metrics.RootMeanSquaredError()])
compile_model(model)
With this, we complete the compilation of our network and are ready to start training.
6. Train the model
Now that we created and compiled our dense neural network, we can start training it.
One additional concept we need to introduce though, is the batch_size.
This defines how many samples from the training data will be used to estimate the error gradient before the model weights are updated.
Larger batches will produce better, more accurate gradient estimates but also less frequent updates of the weights.
Here we are going to use a batch size of 32 which is a common starting point.
history = model.fit(X_train, y_train,
batch_size=32,
epochs=200,
verbose=2)
We can plot the training process using the history object returned from the model training.
We will create a function for it, because we will make use of this more often in this lesson!
import seaborn as sns
import matplotlib.pyplot as plt
def plot_history(metrics):
"""
Plot the training history
Args:
metrics(str, list): Metric or a list of metrics to plot
"""
history_df = pd.DataFrame.from_dict(history.history)
sns.lineplot(data=history_df[metrics])
plt.xlabel("epochs")
plt.ylabel("RMSE")
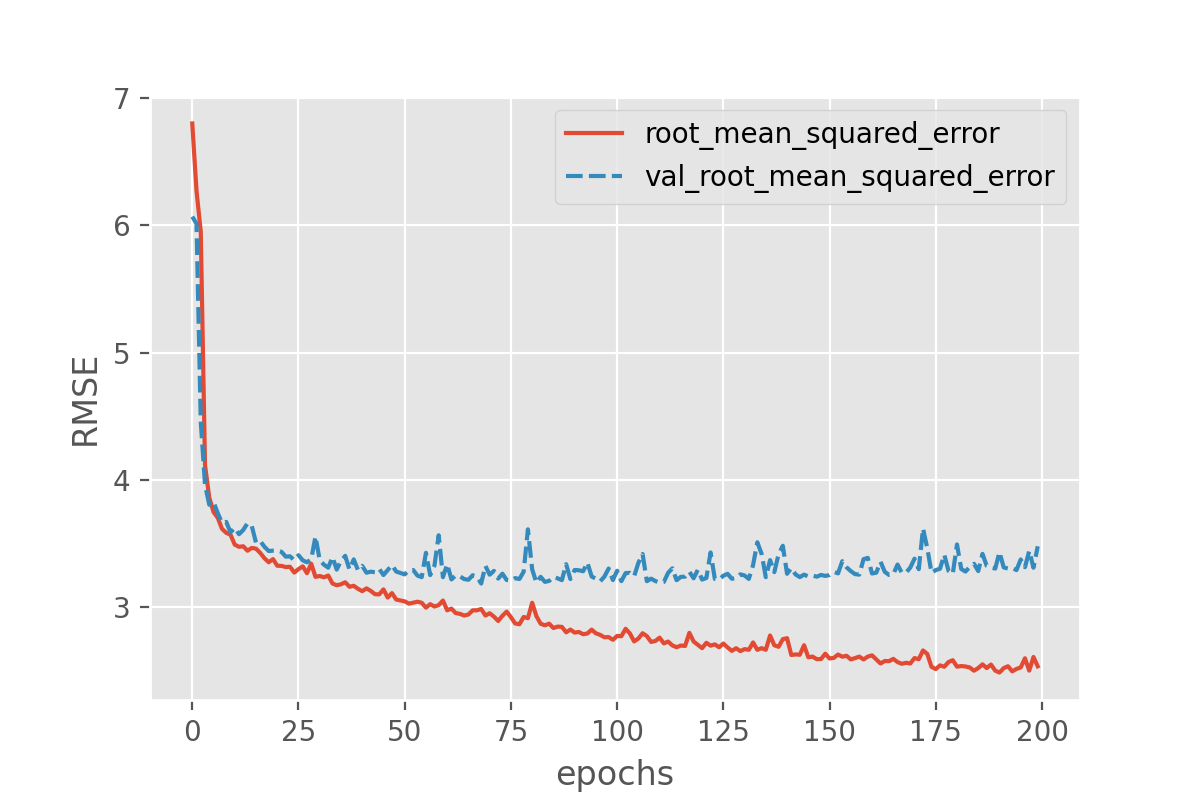
plot_history('root_mean_squared_error')
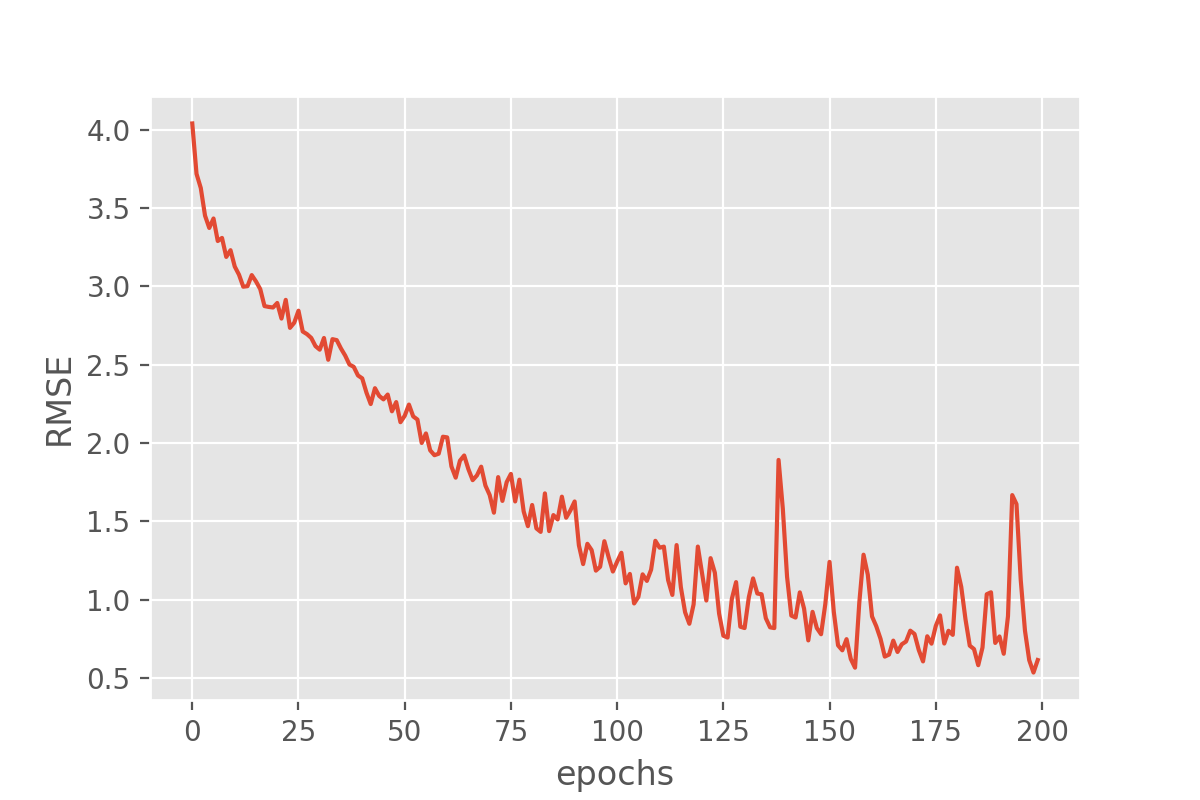
This looks very promising! Our metric (“RMSE”) is dropping nicely and while it maybe keeps fluctuating a bit it does end up at fairly low RMSE values. But the RMSE is just the root mean squared error, so we might want to look a bit more in detail how well our just trained model does in predicting the sunshine hours.
7. Perform a Prediction/Classification
Now that we have our model trained, we can make a prediction with the model before measuring the performance of our neural network.
y_train_predicted = model.predict(X_train)
y_test_predicted = model.predict(X_test)
8. Measure performance
There is not a single way to evaluate how a model performs. But there are at least two very common approaches. For a classification task that is to compute a confusion matrix for the test set which shows how often particular classes were predicted correctly or incorrectly.
For the present regression task, it makes more sense to compare true and predicted values in a scatter plot.
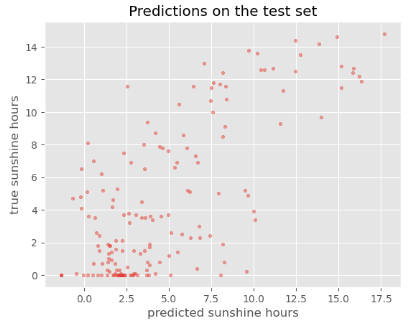
So, let’s look at how the predicted sunshine hour have developed with reference to their ground truth values.
# We define a function that we will reuse in this lesson
def plot_predictions(y_pred, y_true, title):
plt.style.use('ggplot') # optional, that's only to define a visual style
plt.scatter(y_pred, y_true, s=10, alpha=0.5)
plt.xlabel("predicted sunshine hours")
plt.ylabel("true sunshine hours")
plt.title(title)
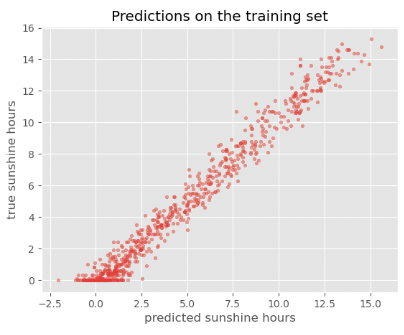
plot_predictions(y_train_predicted, y_train, title='Predictions on the training set')
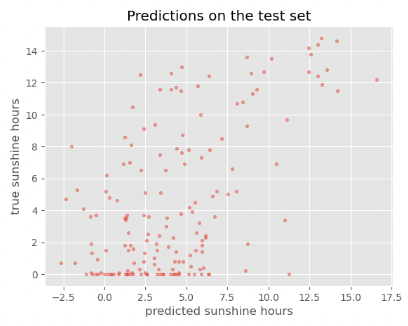
plot_predictions(y_test_predicted, y_test, title='Predictions on the test set')
Exercise: Reflecting on our results
- Is the performance of the model as you expected (or better/worse)?
- Is there a noteable difference between training set and test set? And if so, any idea why?
- (Optional) When developing a model, you will often vary different aspects of your model like which features you use, model parameters and architecture. It is important to settle on a single-number evaluation metric to compare your models.
- What single-number evaluation metric would you choose here and why?
Solution
While the performance on the train set seems reasonable, the performance on the test set is much worse. This is a common problem called overfitting, which we will discuss in more detail later.
Optional exercise: Mean accuracy would be a single-value metric that you can use in this case.
The accuracy on the training set seems fairly good. In fact, considering that the task of predicting the daily sunshine hours is really not easy it might even be surprising how well the model predicts that (at least on the training set). Maybe a little too good? We also see the noticeable difference between train and test set when calculating the exact value of the RMSE:
train_metrics = model.evaluate(X_train, y_train, return_dict=True)
test_metrics = model.evaluate(X_test, y_test, return_dict=True)
print('Train RMSE: {:.2f}, Test RMSE: {:.2f}'.format(train_metrics['root_mean_squared_error'], test_metrics['root_mean_squared_error']))
24/24 [==============================] - 0s 442us/step - loss: 0.7092 - root_mean_squared_error: 0.8421
6/6 [==============================] - 0s 647us/step - loss: 16.4413 - root_mean_squared_error: 4.0548
Train RMSE: 0.84, Test RMSE: 4.05
For those experienced with (classical) machine learning this might look familiar. The plots above expose the signs of overfitting which means that the model has to some extent memorized aspects of the training data. As a result, it makes much more accurate predictions on the training data than on unseen test data.
Overfitting also happens in classical machine learning, but there it is usually interpreted as the model having more parameters than the training data would justify (say, a decision tree with too many branches for the number of training instances). As a consequence one would reduce the number of parameters to avoid overfitting. In deep learning the situation is slightly different. It can - as for classical machine learning - also be a sign of having a too big model, meaning a model with too many parameters (layers and/or nodes). However, in deep learning higher number of model parameters are often still considered acceptable and models often perform best (in terms of prediction accuracy) when they are at the verge of overfitting. So, in a way, training deep learning models is always a bit like playing with fire…
9. Tune hyperparameters
Set expectations: How difficult is the defined problem?
Before we dive deeper into handling overfitting and (trying to) improving the model performance, let us ask the question: How well must a model perform before we consider it a good model?
Now that we defined a problem (predict tomorrow’s sunshine hours), it makes sense to develop an intuition for how difficult the posed problem is. Frequently, models will be evaluated against a so called baseline. A baseline can be the current standard in the field or if such a thing does not exist it could also be an intuitive first guess or toy model. The latter is exactly what we would use for our case.
Maybe the simplest sunshine hour prediction we can easily do is: Tomorrow we will have the same number of sunshine hours as today. (sounds very naive, but for many observables such as temperature this is already a fairly good predictor)
We can take the BASEL_sunshine column of our data, because this contains the sunshine hours from one day before what we have as a label.
y_baseline_prediction = X_test['BASEL_sunshine']
plot_predictions(y_baseline_prediction, y_test, title='Baseline predictions on the test set')
It is difficult to interpret from this plot whether our model is doing better than the baseline. We can also have a look at the RMSE:
from sklearn.metrics import mean_squared_error
rmse_baseline = mean_squared_error(y_test, y_baseline_prediction, squared=False)
print('Baseline:', rmse_baseline)
print('Neural network: ', test_metrics['root_mean_squared_error'])
Baseline: 3.877323350410224
Neural network: 4.077792167663574
Judging from the numbers alone, our neural network prediction would be performing worse than the baseline.
Exercise: Baseline
- Looking at this baseline: Would you consider this a simple or a hard problem to solve?
- (Optional) Can you think of other baselines?
Solution
- This really depends on your definition of hard! The baseline gives a more accurate prediction than just randomly predicting a number, so the problem is not impossible to solve with machine learning. However, given the structure of the data and our expectations with respect to quality of prediction, it may remain hard to find a good algorithm which exceeds our baseline by orders of magnitude.
- There are a lot of possible answers. A slighly more complicated baseline would be to take the average over the last couple of days.
Watch your model training closely
As we saw when comparing the predictions for the training and the test set, deep learning models are prone to overfitting. Instead of iterating through countless cycles of model trainings and subsequent evaluations with a reserved test set, it is common practice to work with a second split off dataset to monitor the model during training. This is the validation set which can be regarded as a second test set. As with the test set, the datapoints of the validation set are not used for the actual model training itself. Instead, we evaluate the model with the validation set after every epoch during training, for instance to stop if we see signs of clear overfitting. Since we are adapting our model (tuning our hyperparameters) based on this validation set, it is very important that it is kept separate from the test set. If we used the same set, we would not know whether our model truly generalizes or is only overfitting.
Test vs. validation set
Not everybody agrees on the terminology of test set versus validation set. You might find examples in literature where these terms are used the other way around.
We are sticking to the definition that is consistent with the Keras API. In there, the validation set can be used during training, and the test set is reserved for afterwards.
Let’s give this a try!
We need to initiate a new model – otherwise Keras will simply assume that we want to continue training the model we already trained above.
model = create_nn()
compile_model(model)
But now we train it with the small addition of also passing it our validation set:
history = model.fit(X_train, y_train,
batch_size=32,
epochs=200,
validation_data=(X_val, y_val))
With this we can plot both the performance on the training data and on the validation data!
plot_history(['root_mean_squared_error', 'val_root_mean_squared_error'])
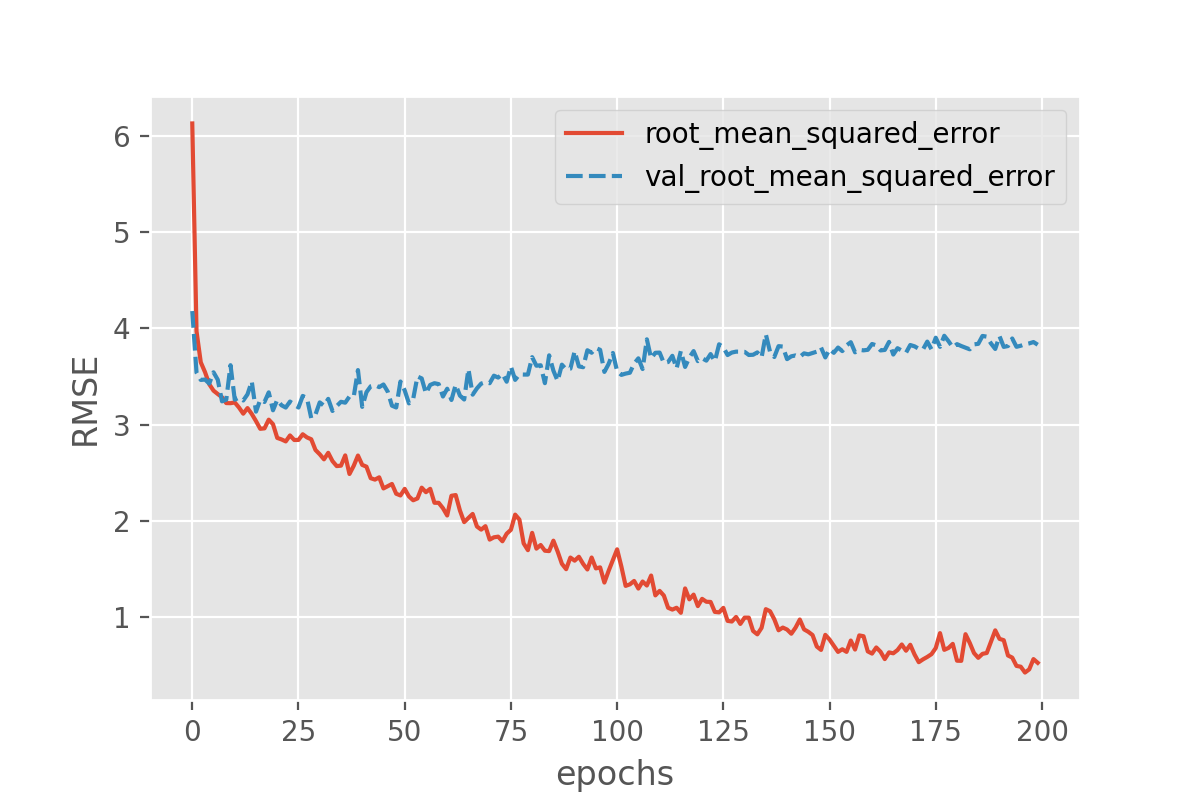
Exercise: plot the training progress.
- Is there a difference between the training and validation data? And if so, what would this imply?
- (Optional) Take a pen and paper, draw the perfect training and validation curves. (This may seem trivial, but it will trigger you to think about what you actually would like to see)
Solution
The difference between training and validation data shows that something is not completely right here. The model predictions on the validation set quickly seem to reach a plateau while the performance on the training set keeps improving. That is a common signature of overfitting.
Optional: Ideally you would like the training and validation curves to be identical and slope down steeply to 0. After that the curves will just consistently stay at 0.
Counteract model overfitting
Overfitting is a very common issue and there are many strategies to handle it. Most similar to classical machine learning might to reduce the number of parameters.
Exercise: Try to reduce the degree of overfitting by lowering the number of parameters
We can keep the network architecture unchanged (2 dense layers + a one-node output layer) and only play with the number of nodes per layer. Try to lower the number of nodes in one or both of the two dense layers and observe the changes to the training and validation losses. If time is short: Suggestion is to run one network with only 10 and 5 nodes in the first and second layer.
- Is it possible to get rid of overfitting this way?
- Does the overall performance suffer or does it mostly stay the same?
- How low can you go with the number of parameters without notable effect on the performance on the validation set?
Solution
def create_nn(nodes1=100, nodes2=50): # Input layer inputs = keras.layers.Input(shape=(X_data.shape[1],), name='input') # Dense layers layers_dense = keras.layers.Dense(nodes1, 'relu')(inputs) layers_dense = keras.layers.Dense(nodes2, 'relu')(layers_dense) # Output layer outputs = keras.layers.Dense(1)(layers_dense) return keras.Model(inputs=inputs, outputs=outputs, name="model_small") model = create_nn(10, 5) model.summary()Model: "model_small" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input (InputLayer) [(None, 89)] 0 _________________________________________________________________ dense_9 (Dense) (None, 10) 900 _________________________________________________________________ dense_10 (Dense) (None, 5) 55 _________________________________________________________________ dense_11 (Dense) (None, 1) 6 ================================================================= Total params: 961 Trainable params: 961 Non-trainable params: 0compile_model(model) history = model.fit(X_train, y_train, batch_size = 32, epochs = 200, validation_data=(X_val, y_val)) plot_history(['root_mean_squared_error', 'val_root_mean_squared_error'])
There is no single correct solution here. But you will have noticed that the number of nodes can be reduced quite a bit!
In general, it quickly becomes a very complicated search for the right “sweet spot”, i.e. the settings for which overfitting will be (nearly) avoided but which still performes equally well.
We saw that reducing the number of parameters can be a strategy to avoid overfitting. In practice, however, this is usually not the (main) way to go when it comes to deep learning. One reason is, that finding the sweet spot can be really hard and time consuming. And it has to be repeated every time the model is adapted, e.g. when more training data becomes available.
Sweet Spots
Note: There is no single correct solution here. But you will have noticed that the number of nodes can be reduced quite a bit! In general, it quickly becomes a very complicated search for the right “sweet spot”, i.e. the settings for which overfitting will be (nearly) avoided but which still performes equally well.
Early stopping: stop when things are looking best
Arguable the most common technique to avoid (severe) overfitting in deep learning is called early stopping. As the name suggests, this technique just means that you stop the model training if things do not seem to improve anymore. More specifically, this usually means that the training is stopped if the validation loss does not (notably) improve anymore. Early stopping is both intuitive and effective to use, so it has become a standard addition for model training.
To better study the effect, we can now safely go back to models with many (too many?) parameters:
model = create_nn()
compile_model(model)
To apply early stopping during training it is easiest to use Keras EarlyStopping class.
This allows to define the condition of when to stop training. In our case we will say when the validation loss is lowest.
However, since we have seen quiet some fluctuation of the losses during training above we will also set patience=10 which means that the model will stop training if the validation loss has not gone down for 10 epochs.
from tensorflow.keras.callbacks import EarlyStopping
earlystopper = EarlyStopping(
monitor='val_loss',
patience=10
)
history = model.fit(X_train, y_train,
batch_size = 32,
epochs = 200,
validation_data=(X_val, y_val),
callbacks=[earlystopper])
As before, we can plot the losses during training:
plot_history(['root_mean_squared_error', 'val_root_mean_squared_error'])
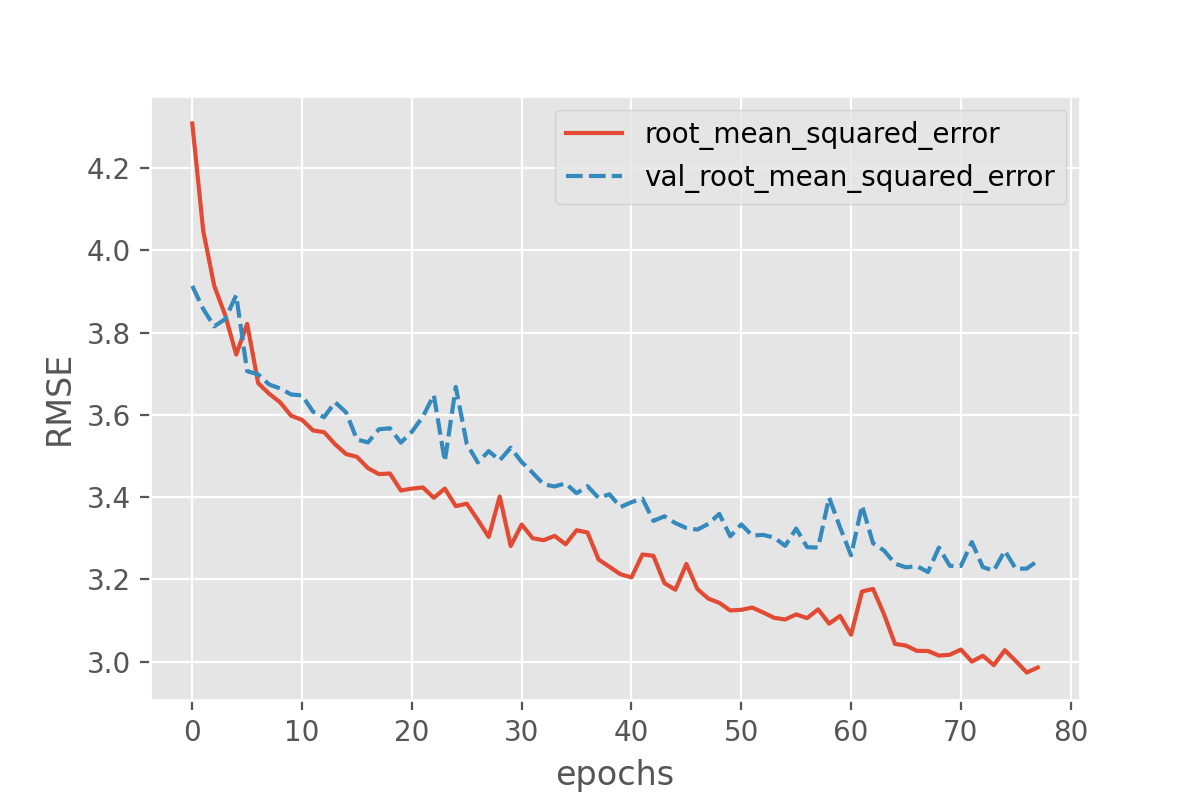
This still seems to reveal the onset of overfitting, but the training stops before the discrepancy between training and validation loss can grow further. Despite avoiding severe cases of overfitting, early stopping has the additional advantage that the number of training epochs will be regulated automatically. Instead of comparing training runs for different number of epochs, early stopping allows to simply set the number of epochs to a desired maximum value.
What might be a bit unintuitive is that the training runs might now end very rapidly. This might spark the question: have we really reached an optimum yet? And often the answer to this is “no”, which is why early stopping frequently is combined with other approaches to avoid overfitting. Overfitting means that a model (seemingly) performs better on seen data compared to unseen data. One then often also says that it does not “generalize” well. Techniques to avoid overfitting, or to improve model generalization, are termed regularization techniques and we will come back to this in episode 4.
BatchNorm: the “standard scaler” for deep learning
A very common step in classical machine learning pipelines is to scale the features, for instance by using sckit-learn’s StandardScaler.
This can in principle also be done for deep learning.
An alternative, more common approach, is to add BatchNormalization layers (documentation of the batch normalization layer) which will learn how to scale the input values.
Similar to dropout, batch normalization is available as a network layer in Keras and can be added to the network in a similar way.
It does not require any additional parameter setting.
from tensorflow.keras.layers import BatchNormalization
The BatchNormalization can be inserted as yet another layer into the architecture.
def create_nn():
# Input layer
inputs = keras.layers.Input(shape=(X_data.shape[1],), name='input')
# Dense layers
layers_dense = keras.layers.BatchNormalization()(inputs)
layers_dense = keras.layers.Dense(100, 'relu')(layers_dense)
layers_dense = keras.layers.Dense(50, 'relu')(layers_dense)
# Output layer
outputs = keras.layers.Dense(1)(layers_dense)
# Defining the model and compiling it
return keras.Model(inputs=inputs, outputs=outputs, name="model_batchnorm")
model = create_nn()
compile_model(model)
model.summary()
This new layer appears in the model summary as well.
Model: "model_batchnorm"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 89)] 0
_________________________________________________________________
batch_normalization (BatchNo (None, 89) 356
_________________________________________________________________
dense (Dense) (None, 100) 9000
_________________________________________________________________
dense_1 (Dense) (None, 50) 5050
_________________________________________________________________
dense_2 (Dense) (None, 1) 51
=================================================================
Total params: 14,457
Trainable params: 14,279
Non-trainable params: 178
We can train the model again as follows:
history = model.fit(X_train, y_train,
batch_size = 32,
epochs = 1000,
validation_data=(X_val, y_val),
callbacks=[earlystopper])
plot_history(['root_mean_squared_error', 'val_root_mean_squared_error'])
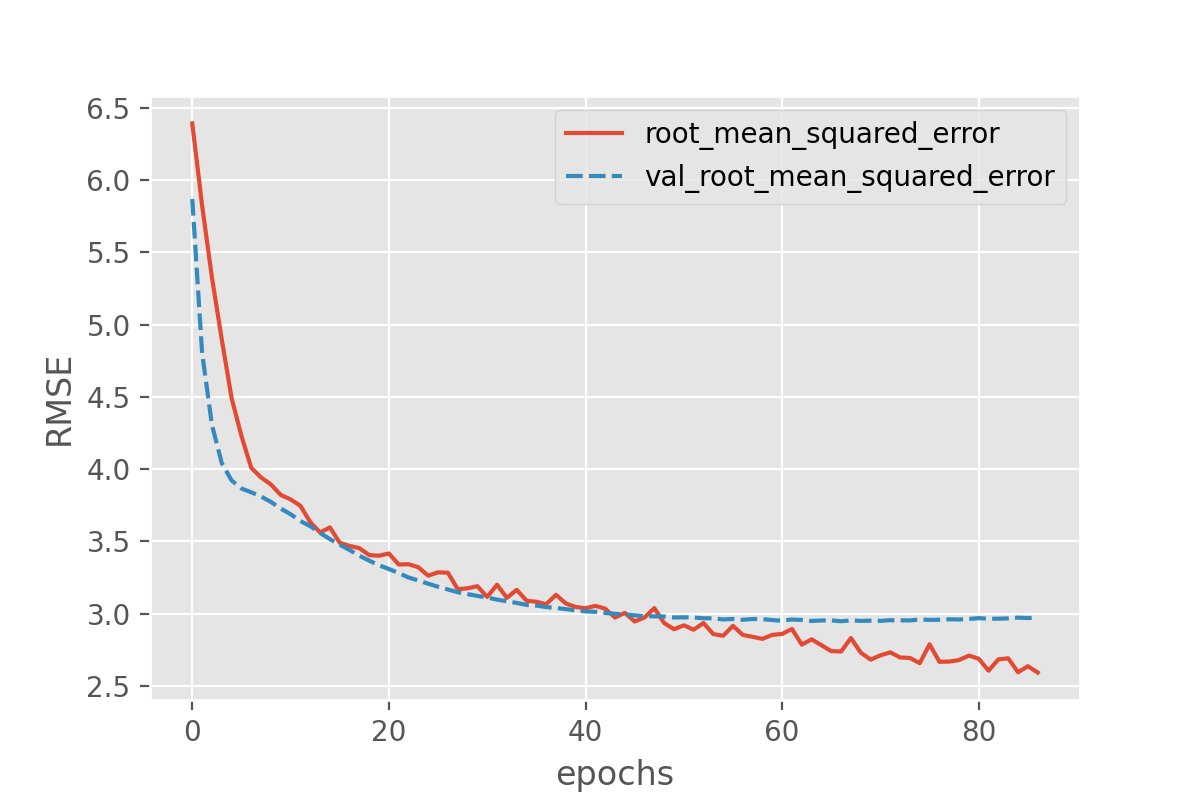
Batchnorm parameters
You may have noticed that the number of parameters of the Batchnorm layers corresponds to 4 parameters per input node. These are the moving mean, moving standard deviation, additional scaling factor (gamma) and offset factor (beta). There is a difference in behavior for Batchnorm between training and prediction time. During training time, the data is scaled with the mean and standard deviation of the batch. During prediction time, the moving mean and moving standard deviation of the training set is used instead. The additional parameters gamma and beta are introduced to allow for more flexibility in output values, and are used in both training and prediction,
Run on test set and compare to naive baseline
It seems that no matter what we add, the overall loss does not decrease much further (we at least avoided overfitting though!). Let us again plot the results on the test set:
y_test_predicted = model.predict(X_test)
plot_predictions(y_test_predicted, y_test, title='Predictions on the test set')
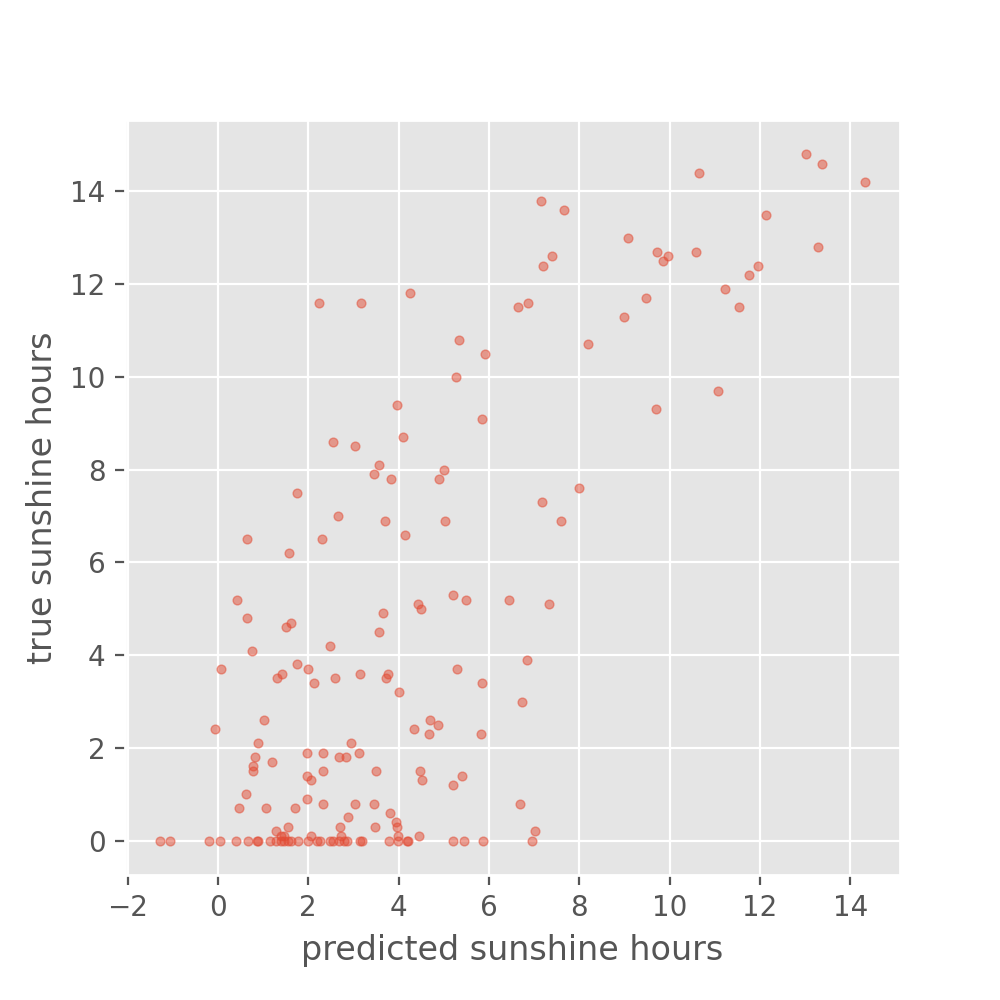
Well, the above is certainly not perfect. But how good or bad is this? Maybe not good enough to plan your picnic for tomorrow. But let’s better compare it to the naive baseline we created in the beginning. What would you say, did we improve on that?
Exercise: Simplify the model and add data
You may have been wondering why we are including weather observations from multiple cities to predict sunshine hours only in Basel. The weather is a complex phenomenon with correlations over large distances and time scales, but what happens if we limit ourselves to only one city?
- Since we will be reducing the number of features quite significantly, we should afford to include more data. Instead of using only 3 years, use 8 or 9 years!
- Remove all cities from the training data that are not for Basel. You can use something like:
cols = [c for c in X_data.columns if c[:5] == 'BASEL'] X_data = X_data[cols]- Now rerun the last model we defined which included the BatchNorm layer. Recreate the scatter plot comparing your prediction with the baseline prediction based on yesterday’s sunshine hours, and compute also the RMSE. Note that even though we will use many more observations than previously, the network should still train quickly because we reduce the number of features (columns). Is the prediction better compared to what we had before?
- (Optional) Try to train a model on all years that are available, and all features from all cities. How does it perform?
Solution
Use 9 years out of the total dataset. This means 3 times as many rows as we used previously, but by removing columns not containing “BASEL” we reduce the number of columns from 89 to 11.
nr_rows = 365*9 # data X_data = data.loc[:nr_rows].drop(columns=['DATE', 'MONTH']) # labels (sunshine hours the next day) y_data = data.loc[1:(nr_rows + 1)]["BASEL_sunshine"] # only use columns with 'BASEL' cols = [c for c in X_data.columns if c[:5] == 'BASEL'] X_data = X_data[cols]Do the train-test-validation split:
X_train, X_holdout, y_train, y_holdout = train_test_split(X_data, y_data, test_size=0.3, random_state=0) X_val, X_test, y_val, y_test = train_test_split(X_holdout, y_holdout, test_size=0.5, random_state=0)
Create the network. We can re-use the
create_nnthat we already have. Because we have reduced the number of input features the number of parameters in the network goes down from 14457 to 6137.# create the network and view its summary model = create_nn() compile_model(model) model.summary()Fit with early stopping and output showing performance on validation set:
history = model.fit(X_train, y_train, batch_size = 32, epochs = 1000, validation_data=(X_val, y_val), callbacks=[earlystopper], verbose = 2) plot_history(['root_mean_squared_error', 'val_root_mean_squared_error'])Create a scatter plot to compare with true observations:
y_test_predicted = model.predict(X_test) plot_predictions(y_test_predicted, y_test, title='Predictions on the test set')Compare the mean squared error with baseline prediction. It should be similar or even a little better than what we saw with the larger model!
from sklearn.metrics import mean_squared_error y_baseline_prediction = X_test['BASEL_sunshine'] rmse_nn = mean_squared_error(y_test, y_test_predicted, squared=False) rmse_baseline = mean_squared_error(y_test, y_baseline_prediction, squared=False) print('NN RMSE: {:.2f}, baseline RMSE: {:.2f}'.format(rmse_nn, rmse_baseline))
Tensorboard
If we run many different experiments with different architectures, it can be difficult to keep track of these different models or compare the achieved performance. We can use tensorboard, a framework that keeps track of our experiments and shows graphs like we plotted above. Tensorboard is included in our tensorflow installation by default. To use it, we first need to add a callback to our (compiled) model that saves the progress of training performance in a logs directory:
from tensorflow.keras.callbacks import TensorBoard import datetime log_dir = "logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S") # You can adjust this to add a more meaningful model name tensorboard_callback = TensorBoard(log_dir=log_dir, histogram_freq=1) history = model.fit(X_train, y_train, batch_size = 32, epochs = 200, validation_data=(X_val, y_val), callbacks=[tensorboard_callback], verbose = 2)You can launch the tensorboard interface from a Jupyter notebook, showing all trained models:
%load_ext tensorboard %tensorboard --logdir logs/fitWhich will show an interface that looks something like this:
10. Save model
Now that we have a somewhat acceptable model, let us not forget to save it for future users to benefit from our explorative efforts!
model.save('my_tuned_weather_model')
Outlook
Correctly predicting tomorrow’s sunshine hours is apparently not that simple. Our models get the general trends right, but still predictions vary quite a bit and can even be far off.
Open question: What could be next steps to further improve the model?
With unlimited options to modify the model architecture or to play with the training parameters, deep learning can trigger very extensive hunting for better and better results. Usually models are “well behaving” in the sense that small chances to the architectures also only result in small changes of the performance (if any). It is often tempting to hunt for some magical settings that will lead to much better results. But do those settings exist? Applying common sense is often a good first step to make a guess of how much better could results be. In the present case we might certainly not expect to be able to reliably predict sunshine hours for the next day with 5-10 minute precision. But how much better our model could be exactly, often remains difficult to answer.
- What changes to the model architecture might make sense to explore?
- Ignoring changes to the model architecture, what might notably improve the prediction quality?
Solution
This is on open question. And we don’t actually know how far one could push this sunshine hour prediction (try it out yourself if you like! We’re curious!). But there is a few things that might be worth exploring.
Regarding the model architecture:
- In the present case we do not see a magical silver bullet to suddenly boost the performance. But it might be worth testing if deeper networks do better (more layers).
Other changes that might impact the quality notably:
- The most obvious answer here would be: more data! Even this will not always work (e.g. if data is very noisy and uncorrelated, more data might not add much).
- Related to more data: use data augmentation. By creating realistic variations of the available data, the model might improve as well.
- More data can mean more data points (you can test it yourself by taking more than the 3 years we used here!)
- More data can also mean more features! What about adding the month?
- The labels we used here (sunshine hours) are highly biased, many days with no or nearly no sunshine but few with >10 hours. Techniques such as oversampling or undersampling might handle such biased labels better. Another alternative would be to not only look at data from one day, but use the data of a longer period such as a full week. This will turn the data into time series data which in turn might also make it worth to apply different model architectures…
Key Points
Separate training, validation, and test sets allows monitoring and evaluating your model.
Batchnormalization scales the data as part of the model.
Advanced layer types
Overview
Teaching: 30 min
Exercises: 70 minQuestions
Why do we need different types of layers?
What are good network designs for image data?
What is a convolutional layer?
How can we use different types of layers to prevent overfitting?
Objectives
Understand why convolutional and pooling layers are useful for image data
Implement a convolutional neural network on an image dataset
Use a drop-out layer to prevent overfitting
Different types of layers
Networks are like onions: a typical neural network consists of many layers. In fact, the word deep in Deep Learning refers to the many layers that make the network deep.
So far, we have seen one type of layer, namely the fully connected, or dense layer. This layer is called fully connected, because all input neurons are taken into account by each output neuron. The number of parameters that need to be learned by the network, is thus in the order of magnitude of the number of input neurons times the number of hidden neurons.
However, there are many different types of layers that perform different calculations and take different inputs. In this episode we will take a look at convolutional layers and dropout layers, which are useful in the context of image data, but also in many other types of (structured) data.
Image classification
Keras comes with a few prepared datasets. We have a look at the CIFAR10 dataset, which is a widely known dataset for image classification.
from tensorflow import keras
(train_images, train_labels), (test_images, test_labels) = keras.datasets.cifar10.load_data()
CIFAR-10
The CIFAR-10 dataset consists of images of 10 different classes: airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. It is widely used as a benchmark dataset for image classification. The low resolution of the images in the dataset allows for quick loading and testing models.
For more information about this dataset and how it was collected you can check out Learning Multiple Layers of Features from Tiny Images by Alex Krizhevsky, 2009.
CERTIFICATE_VERIFY_FAILED error when downloading CIFAR-10 dataset
When loading the CIFAR-10 dataset, you might get the following error:
[SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: certificate has expired (_ssl.c:1125)You can solve this error by adding this to your notebook:
import ssl ssl._create_default_https_context = ssl._create_unverified_context
We take a small sample of the data as training set for demonstration purposes.
n = 5000
train_images = train_images[:n]
train_labels = train_labels[:n]
Explore the data
Familiarize yourself with the CIFAR10 dataset. To start, consider the following questions:
- What is the dimension of a single data point? What do you think the dimensions mean?
- What is the range of values that your input data takes?
- What is the shape of the labels, and how many labels do we have?
- (Optional) We are going to build a new architecture from scratch to get you familiar with the convolutional neural network basics. But in the real world you wouldn’t do that. So the challenge is: Browse the web for (more) existing architectures or pre-trained models that are likely to work well on this type of data. Try to understand why they work well for this type of data.
Solution
To explore the dimensions of the input data:
train_images.shape(5000, 32, 32, 3)The first value,
5000, is the number of training images that we have selected. The remainder of the shape, namely32, 32, 3), denotes the dimension of one image. The last value 3 is typical for color images, and stands for the three color channels Red, Green, Blue. We are left with32, 32. This denotes the width and height of our input image in number of pixels. By convention, the first entry refers to the height, the second to the width of the image. In this case, we observe a quadratic image where height equals width.We can find out the range of values of our input data as follows:
train_images.min(), train_images.max()(0, 255)So the values of the three channels range between
0and255.Lastly, we inspect the dimension of the labels:
train_labels.shape(5000, 1)So we have, for each image, a single value denoting the label. To find out what the possible values of these labels are:
train_labels.min(), train_labels.max()(0, 9)The values of the labels range between
0and9, denoting 10 different classes.
The training set consists of 50000 images of 32x32 pixels and 3 channels (RGB values). The RGB values are between 0 and 255. For input of neural networks, it is better to have small input values. So we normalize our data between 0 and 1:
train_images = train_images / 255.0
test_images = test_images / 255.0
The labels are single numbers denoting the class. We map the class numbers back to the class names, taken from the documentation:
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
Now we can plot a sample of the training images, using the plt.imshow function.
import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.axis('off')
plt.title(class_names[train_labels[i,0]])
plt.show()

Convolutional layers
In the previous episodes, we used ‘fully connected layers’ , that connected all input values of a layer to all outputs of a layer. This results in many connections, and thus weights to be learned, in the network. Note that our input dimension is now quite high (even with small pictures of 32x32 pixels), we have:
dim = train_images.shape[1] * train_images.shape[2] * train_images.shape[3]
print(dim)
3072
Number of parameters
Suppose we create a single Dense (fully connected) layer with 100 hidden units that connect to the input pixels, how many parameters does this layer have?
Solution
Each entry of the input dimensions, i.e. the
shapeof one single data point, is connected with 100 neurons of our hidden layer, and each of these neurons has a bias term associated to it. So we have307300parameters to learn.width, height = (32, 32) n_hidden_neurons = 100 n_bias = 100 n_input_items = width * height * 3 n_parameters = (n_input_items * n_hidden_neurons) + n_bias n_parameters307300We can also check this by building the layer in Keras:
inputs = keras.Input(shape=dim) outputs = keras.layers.Dense(100)(inputs) model = keras.models.Model(inputs=inputs, outputs=outputs) model.summary()Model: "model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) [(None, 3072)] 0 _________________________________________________________________ dense (Dense) (None, 100) 307300 ================================================================= Total params: 307,300 Trainable params: 307,300 Non-trainable params: 0 _________________________________________________________________
We can decrease the number of units in our hidden layer, but this also decreases the number of patterns our network can remember. Moreover, if we increase the image size, the number of weights will ‘explode’, even though the task of recognizing large images is not necessarily more difficult than the task of recognizing small images.
The solution is that we make the network learn in a ‘smart’ way. The features that we learn should be similar both for small and large images, and similar features (e.g. edges, corners) can appear anywhere in the image (in mathematical terms: translation invariant). We do this by making use of a concepts from image processing that precede Deep Learning.
A convolution matrix, or kernel, is a matrix transformation that we ‘slide’ over the image to calculate features at each position of the image. For each pixel, we calculate the matrix product between the kernel and the pixel with its surroundings. A kernel is typically small, between 3x3 and 7x7 pixels. We can for example think of the 3x3 kernel:
[[-1, -1, -1],
[0, 0, 0]
[1, 1, 1]]
This kernel will give a high value to a pixel if it is on a horizontal border between dark and light areas. Note that for RGB images, the kernel should also have a depth of 3.
In the following image, we see the effect of such a kernel on the values of a single-channel image. The red cell in the output matrix is the result of multiplying and summing the values of the red square in the input, and the kernel. Applying this kernel to a real image shows that it indeed detects horizontal edges.
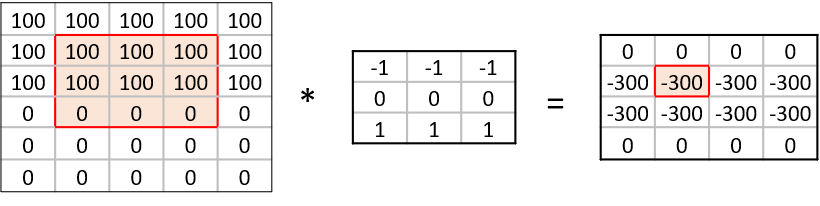
In our convolutional layer our hidden units are a number of convolutional matrices (or kernels), where the values of the matrices are the weights that we learn in the training process. The output of a convolutional layer is an ‘image’ for each of the kernels, that gives the output of the kernel applied to each pixel.
Playing with convolutions
Convolutions applied to images can be hard to grasp at first. Fortunately there are resources out there that enable users to interactively play around with images and convolutions:
- Image kernels explained shows how different convolutions can achieve certain effects on an image, like sharpening and blurring.
- The convolutional neural network cheat sheet shows animated examples of the different components of convolutional neural nets
Border pixels
What, do you think, happens to the border pixels when applying a convolution?
Solution
There are different ways of dealing with border pixels. You can ignore them, which means that your output image is slightly smaller then your input. It is also possible to ‘pad’ the borders, e.g. with the same value or with zeros, so that the convolution can also be applied to the border pixels. In that case, the output image will have the same size as the input image.
Number of model parameters
Suppose we apply a convolutional layer with 100 kernels of size 3 * 3 * 3 (the last dimension applies to the rgb channels) to our images of 32 * 32 * 3 pixels. How many parameters do we have? Assume, for simplicity, that the kernels do not use bias terms. Compare this to the answer of the previous exercise
Solution
We have 100 matrices with 3 * 3 * 3 = 27 values each so that gives 27 * 100 = 2700 weights. This is a magnitude of 100 less than the fully connected layer with 100 units! Nevertheless, as we will see, convolutional networks work very well for image data. This illustrates the expressiveness of convolutional layers.
So let us look at a network with a few convolutional layers. We need to finish with a Dense layer to connect the output cells of the convolutional layer to the outputs for our classes.
inputs = keras.Input(shape=train_images.shape[1:])
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs)
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x)
x = keras.layers.Flatten()(x)
outputs = keras.layers.Dense(10)(x)
model = keras.Model(inputs=inputs, outputs=outputs, name="cifar_model_small")
model.summary()
Convolutional Neural Network
Inspect the network above:
- What do you think is the function of the
Flattenlayer?- Which layer has the most parameters? Do you find this intuitive?
- (optional) Pick a model from https://paperswithcode.com/sota/image-classification-on-cifar-10 . Try to understand how it works.
Solution
- The Flatten layer converts the 28x28x50 output of the convolutional layer into a single one-dimensional vector, that can be used as input for a dense layer.
- The last dense layer has the most parameters. This layer connects every single output ‘pixel’ from the convolutional layer to the 10 output classes. That results in a large number of connections, so a large number of parameters. This undermines a bit the expressiveness of the convolutional layers, that have much fewer parameters.
Often in convolutional neural networks, the convolutional layers are intertwined with Pooling layers. As opposed to the convolutional layer, the pooling layer actually alters the dimensions of the image and reduces it by a scaling factor. It is basically decreasing the resolution of your picture. The rationale behind this is that higher layers of the network should focus on higher-level features of the image. By introducing a pooling layer, the subsequent convolutional layer has a broader ‘view’ on the original image.
Let’s put it into practice. We compose a Convolutional network with two convolutional layers and two pooling layers.
inputs = keras.Input(shape=train_images.shape[1:])
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs)
x = keras.layers.MaxPooling2D((2, 2))(x)
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(50, activation='relu')(x)
outputs = keras.layers.Dense(10)(x)
model = keras.Model(inputs=inputs, outputs=outputs, name="cifar_model_small")
model.summary()
Model: "cifar_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_6 (InputLayer) [(None, 32, 32, 3)] 0
conv2d_13 (Conv2D) (None, 30, 30, 50) 1400
max_pooling2d_8 (MaxPooling (None, 15, 15, 50) 0
2D)
conv2d_14 (Conv2D) (None, 13, 13, 50) 22550
max_pooling2d_9 (MaxPooling (None, 6, 6, 50) 0
2D)
conv2d_15 (Conv2D) (None, 4, 4, 50) 22550
flatten_5 (Flatten) (None, 800) 0
dense_9 (Dense) (None, 50) 40050
dense_10 (Dense) (None, 10) 510
=================================================================
Total params: 87,060
Trainable params: 87,060
Non-trainable params: 0
_________________________________________________________________
We compile the model using the adam optimizer (other optimizers could also be used here!). Similar to the penguin classification task, we will use the crossentropy function to calculate the model’s loss. This loss function is appropriate to use when the data has two or more label classes.
To calculate crossentropy loss for data that has its classes represented by integers (i.e., not one-hot encoded), we use the SparseCategoricalCrossentropy() function:
model.compile(optimizer='adam',
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
We then train the model for 10 epochs:
history = model.fit(train_images, train_labels, epochs=10,
validation_data=(test_images, test_labels))
We can plot the training process using the history:
import seaborn as sns
import pandas as pd
history_df = pd.DataFrame.from_dict(history.history)
sns.lineplot(data=history_df[['accuracy', 'val_accuracy']])
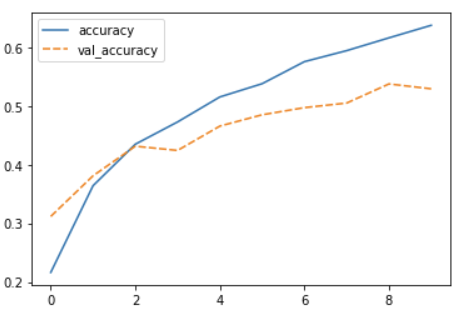
sns.lineplot(data=history_df[['loss', 'val_loss']])
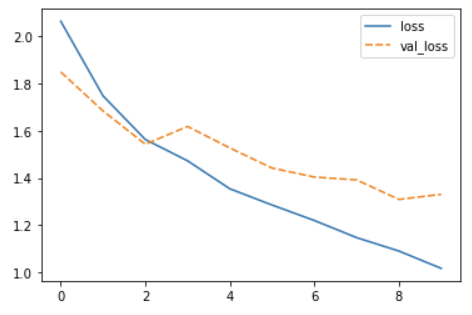
It seems that the model is overfitting somewhat, because the validation accuracy and loss stagnates.
Network depth
What, do you think, will be the effect of adding a convolutional layer to your model? Will this model have more or fewer parameters? Try it out. Create a
modelthat has an additionalConv2dlayer with 50 filters after the last MaxPooling2D layer. Train it for 20 epochs and plot the results.HINT: The model definition that we used previously needs to be adjusted as follows:
inputs = keras.Input(shape=train_images.shape[1:]) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs) x = keras.layers.MaxPooling2D((2, 2))(x) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x) x = keras.layers.MaxPooling2D((2, 2))(x) # Add your extra layer here x = keras.layers.Flatten()(x) x = keras.layers.Dense(50, activation='relu')(x) outputs = keras.layers.Dense(10)(x)Solution
We add an extra Conv2D layer after the second pooling layer:
inputs = keras.Input(shape=train_images.shape[1:]) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs) x = keras.layers.MaxPooling2D((2, 2))(x) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x) x = keras.layers.MaxPooling2D((2, 2))(x) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x) x = keras.layers.Flatten()(x) x = keras.layers.Dense(50, activation='relu')(x) outputs = keras.layers.Dense(10)(x) model = keras.Model(inputs=inputs, outputs=outputs, name="cifar_model")With the model defined above, we can inspect the number of parameters:
model.summary()Model: "cifar_model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_7 (InputLayer) [(None, 32, 32, 3)] 0 conv2d_16 (Conv2D) (None, 30, 30, 50) 1400 max_pooling2d_10 (MaxPoolin (None, 15, 15, 50) 0 g2D) conv2d_17 (Conv2D) (None, 13, 13, 50) 22550 max_pooling2d_11 (MaxPoolin (None, 6, 6, 50) 0 g2D) conv2d_18 (Conv2D) (None, 4, 4, 50) 22550 flatten_6 (Flatten) (None, 800) 0 dense_11 (Dense) (None, 50) 40050 dense_12 (Dense) (None, 10) 510 ================================================================= Total params: 87,060 Trainable params: 87,060 Non-trainable params: 0 _________________________________________________________________The number of parameters has decreased by adding this layer. We can see that the conv layer decreases the resolution from 6x6 to 4x4, as a result, the input of the Dense layer is smaller than in the previous network.
To train the network and plot the results:
model.compile(optimizer='adam', loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True), metrics=['accuracy']) history = model.fit(train_images, train_labels, epochs=20, validation_data=(test_images, test_labels)) history_df = pd.DataFrame.from_dict(history.history) sns.lineplot(data=history_df[['accuracy', 'val_accuracy']])
sns.lineplot(data=history_df[['loss', 'val_loss']])
Other types of data
Convolutional and Pooling layers are also applicable to different types of data than image data. Whenever the data is ordered in a (spatial) dimension, and translation invariant features are expected to be useful, convolutions can be used. Think for example of time series data from an accelerometer, audio data for speech recognition, or 3d structures of chemical compounds.
Why and when to use convolutional neural networks
- Would it make sense to train a convolutional neural network (CNN) on the penguins dataset and why?
- Would it make sense to train a CNN on the weather dataset and why?
- (Optional) Can you think of a different machine learning task that would benefit from a CNN architecture?
Solution
- No that would not make sense. Convolutions only work when the features of the data can be ordered in a meaningful way. Pixels for exmaple are ordered in a spatial dimension. This kind of order cannot be applied to the features of the penguin dataset. If we would have pictures or audio recordings of the penguins as input data it would make sense to use a CNN architecture.
- It would make sense, but only if we approach the problem from a different angle then we did before. Namely, 1D convolutions work quite well on sequential data such as timeseries. If we have as our input a matrix of the different weather conditions over time in the past x days, a CNN would be suited to quickly grasp the temporal relationship over days.
- Some example domains in which CNNs are applied:
- Text data
- Timeseries, specifically audio
- Molecular structures
Dropout
Note that the training loss continues to decrease, while the validation loss stagnates, and even starts to increase over the course of the epochs. Similarly, the accuracy for the validation set does not improve anymore after some epochs. This means we are overfitting on our training data set.
Techniques to avoid overfitting, or to improve model generalization, are termed regularization techniques.
One of the most versatile regularization technique is dropout (Srivastava et al., 2014).
Dropout essentially means that during each training cycle a random fraction of the dense layer nodes are turned off. This is described with the dropout rate between 0 and 1 which determines the fraction of nodes to silence at a time.
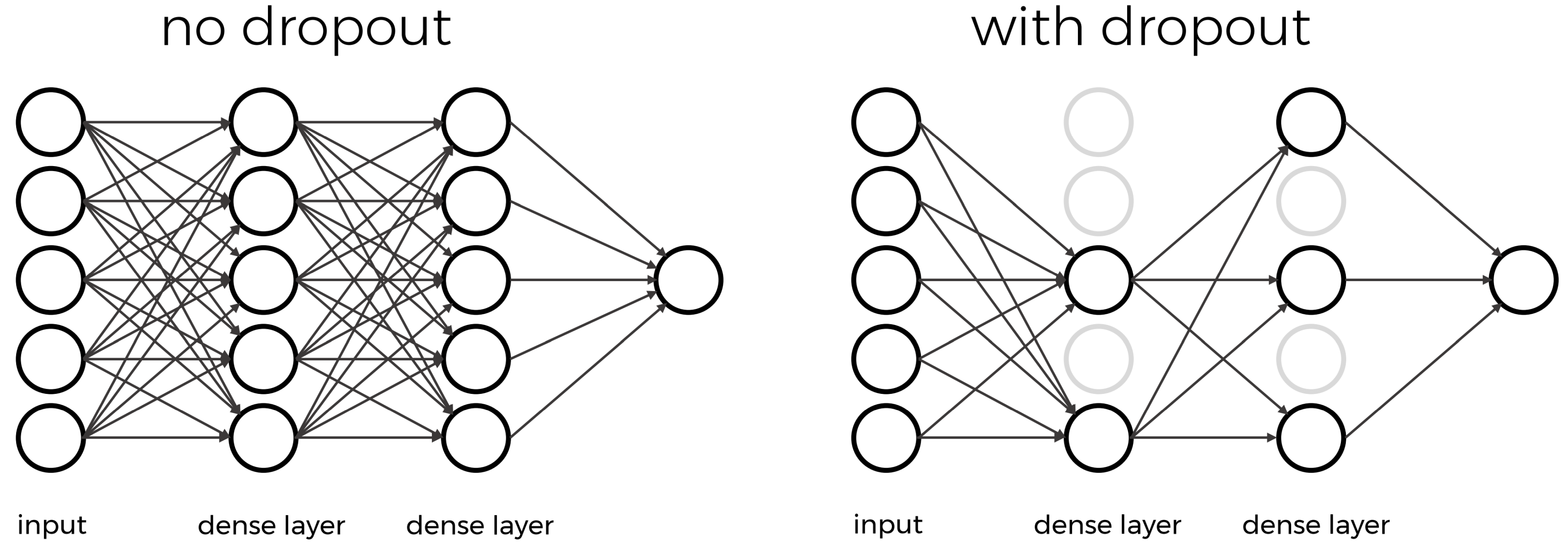 The intuition behind dropout is that it enforces redundancies in the network by constantly removing different elements of a network. The model can no longer rely on individual nodes and instead must create multiple “paths”. In addition, the model has to make predictions with much fewer nodes and weights (connections between the nodes).
As a result, it becomes much harder for a network to memorize particular features. At first this might appear a quiet drastic approach which affects the network architecture strongly.
In practice, however, dropout is computationally a very elegant solution which does not affect training speed. And it frequently works very well.
The intuition behind dropout is that it enforces redundancies in the network by constantly removing different elements of a network. The model can no longer rely on individual nodes and instead must create multiple “paths”. In addition, the model has to make predictions with much fewer nodes and weights (connections between the nodes).
As a result, it becomes much harder for a network to memorize particular features. At first this might appear a quiet drastic approach which affects the network architecture strongly.
In practice, however, dropout is computationally a very elegant solution which does not affect training speed. And it frequently works very well.
Important to note: Dropout layers will only randomly silence nodes during training! During a predictions step, all nodes remain active (dropout is off). During training, the sample of nodes that are silenced are different for each training instance, to give all nodes a chance to observe enough training data to learn its weights.
Let us add one dropout layer towards the end of the network, that randomly drops 20% of the input units.
inputs = keras.Input(shape=train_images.shape[1:])
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs)
x = keras.layers.MaxPooling2D((2, 2))(x)
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x)
x = keras.layers.Dropout(0.8)(x) # This is new!
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(50, activation='relu')(x)
outputs = keras.layers.Dense(10)(x)
model_dropout = keras.Model(inputs=inputs, outputs=outputs, name="cifar_model")
model_dropout.summary()
Model: "cifar_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_8 (InputLayer) [(None, 32, 32, 3)] 0
conv2d_19 (Conv2D) (None, 30, 30, 50) 1400
max_pooling2d_12 (MaxPoolin (None, 15, 15, 50) 0
g2D)
conv2d_20 (Conv2D) (None, 13, 13, 50) 22550
max_pooling2d_13 (MaxPoolin (None, 6, 6, 50) 0
g2D)
conv2d_21 (Conv2D) (None, 4, 4, 50) 22550
dropout_2 (Dropout) (None, 4, 4, 50) 0
flatten_7 (Flatten) (None, 800) 0
dense_13 (Dense) (None, 50) 40050
dense_14 (Dense) (None, 10) 510
=================================================================
Total params: 87,060
Trainable params: 87,060
Non-trainable params: 0
_________________________________________________________________
We can see that the dropout does not alter the dimensions of the image, and has zero parameters.
We again compile and train the model.
model_dropout.compile(optimizer='adam',
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
history_dropout = model_dropout.fit(train_images, train_labels, epochs=20,
validation_data=(test_images, test_labels))
And inspect the training results:
history_df = pd.DataFrame.from_dict(history_dropout.history)
history_df['epoch'] = range(1,len(history_df)+1)
history_df = history_df.set_index('epoch')
sns.lineplot(data=history_df[['accuracy', 'val_accuracy']])
test_loss, test_acc = model_dropout.evaluate(test_images, test_labels, verbose=2)
313/313 - 2s - loss: 1.4683 - accuracy: 0.5307
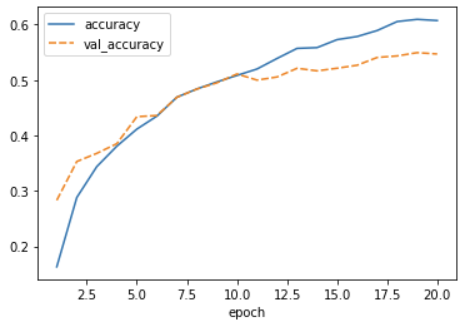
sns.lineplot(data=history_df[['loss', 'val_loss']])
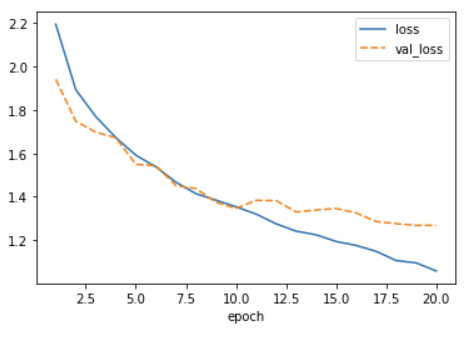
Now we see that the gap between the training accuracy and validation accuracy is much smaller, and that the final accuracy on the validation set is higher than without dropout. Nevertheless, there is still some difference between the training loss and validation loss, so we could experiment with regularization even more.
Vary dropout rate
- What do you think would happen if you lower the dropout rate? Try it out, and see how it affects the model training.
- You are varying the dropout rate and checking its effect on the model performance, what is the term associated to this procedure?
Solution
1. Varying the dropout rate
The code below instantiates and trains a model with varying dropout rates. You can see from the resulting plot that the ideal dropout rate in this case is around 0.45. This is where the test loss is lowest.
- NB1: It takes a while to train these 5 networks.
- NB2: In the real world you should do this with a validation set and not with the test set!
dropout_rates = [0.15, 0.3, 0.45, 0.6, 0.75] test_losses = [] for dropout_rate in dropout_rates: inputs = keras.Input(shape=train_images.shape[1:]) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(inputs) x = keras.layers.MaxPooling2D((2, 2))(x) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x) x = keras.layers.MaxPooling2D((2, 2))(x) x = keras.layers.Conv2D(50, (3, 3), activation='relu')(x) x = keras.layers.Dropout(dropout_rate)(x) x = keras.layers.Flatten()(x) x = keras.layers.Dense(50, activation='relu')(x) outputs = keras.layers.Dense(10)(x) model_dropout = keras.Model(inputs=inputs, outputs=outputs, name="cifar_model") model_dropout.compile(optimizer='adam', loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True), metrics=['accuracy']) model_dropout.fit(train_images, train_labels, epochs=20, validation_data=(test_images, test_labels)) test_loss, test_acc = model_dropout.evaluate(test_images, test_labels) test_losses.append(test_loss) loss_df = pd.DataFrame({'dropout_rate': dropout_rates, 'test_loss': test_losses}) sns.lineplot(data=loss_df, x='dropout_rate', y='test_loss')
2. Term associated to this procedure
This is called hyperparameter tuning.
Key Points
Convolutional layers make efficient reuse of model parameters.
Pooling layers decrease the resolution of your input
Dropout is a way to prevent overfitting