First look at our dataset

Assuming you are familiar with pandas dataframes, in this notebook we look at the necessary steps required before any machine learning takes place. It involves:

• highlighting that it is crucial to inspect the data before building a model

• looking at the variables in the dataset, in particular, differentiate between numerical and categorical variables, which need different preprocessing in most machine learning workflows;

• visualizing the distribution of the variables to gain some insights into the dataset.

Note

To the instructor

Instead of live-coding this notebook, explain the important concepts before ML and show the descriptive statistics. TBC.

Loading the adult census dataset

We use pandas to load the data.

import pandas as pd

adult_census = pd.read_csv("../datasets/adult-census.csv")

adult_census.head()

	age	workclass	education	education-num	marital-status	occupation	relationship	race	sex	capital-gain	capital-loss	hours-per-week	native-country	class
0	25	Private	11th	7	Never-married	Machine-op-inspct	Own-child	Black	Male	0	0	40	United-States	<=50K
1	38	Private	HS-grad	9	Married-civ-spouse	Farming-fishing	Husband	White	Male	0	0	50	United-States	<=50K
2	28	Local-gov	Assoc-acdm	12	Married-civ-spouse	Protective-serv	Husband	White	Male	0	0	40	United-States	>50K
3	44	Private	Some-college	10	Married-civ-spouse	Machine-op-inspct	Husband	Black	Male	7688	0	40	United-States	>50K
4	18	?	Some-college	10	Never-married	?	Own-child	White	Female	0	0	30	United-States	<=50K

Rows and columns

• Each row in the dataframe represents a “sample”. In the field of machine learning or descriptive statistics, commonly used equivalent terms are “record”, “instance”, or “observation”.

• Each column represents a type of information that has been collected and is called a “feature”. In the field of machine learning and descriptive statistics, commonly used equivalent terms are “variable”, “attribute”, or “covariate”.

target_column = "class"
adult_census[target_column].unique()

array([' <=50K', ' >50K'], dtype=object)

Target and input variables

• Our target variable is the column class.

• It has two classes: <=50K (low-revenue) and >50K (high-revenue).

• Thus, the prediction problem is a binary classification problem.

• The columns other than class are input variables for our model.

Categorical and numerical columns

• There are numerical and categorical columns in the data

• Numerical columns take continuous values. Example: "age"

• Categorical columns take a finite number of values. Example: “native-country”

numerical_columns = [
    "age",
    "education-num",
    "capital-gain",
    "capital-loss",
    "hours-per-week",
]
categorical_columns = [
    "workclass",
    "education",
    "marital-status",
    "occupation",
    "relationship",
    "race",
    "sex",
    "native-country",
]
all_columns = numerical_columns + categorical_columns + [target_column]

adult_census = adult_census[all_columns]

We can check the number of samples and the number of columns available in the dataset:

print(
    f"The dataset contains {adult_census.shape[0]} samples and "
    f"{adult_census.shape[1]} columns"
)

The dataset contains 48842 samples and 14 columns

We can compute the number of features by counting the number of columns and subtract 1, since one of the columns is the target.

print(f"The dataset contains {adult_census.shape[1] - 1} features.")

The dataset contains 13 features.

Inspecting the data: individual columns

Before building a predictive model, it is a good idea to look at the data:

• maybe the task you are trying to achieve can be solved without machine learning;

• you need to check that the information you need for your task is actually present in the dataset;

• inspecting the data is a good way to find peculiarities. These can arise during data collection (for example, malfunctioning sensor or missing values), or from the way the data is processed afterwards (for example capped values).

Visually inspecting numerical columns

Let’s look at the distribution of individual features, to get some insights about the data. We can start by plotting histograms, note that this only works for features containing numerical values:

_ = adult_census.hist(figsize=(20, 14))

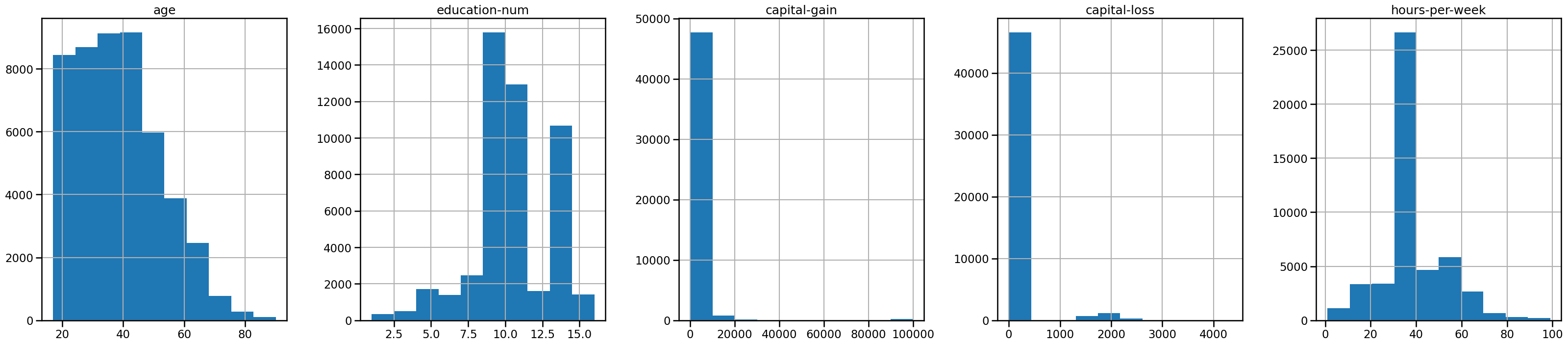
We can already make a few comments about some of the variables:

• "age": there are not that many points for age > 70. The dataset description does indicate that retired people have been filtered out (hours-per-week > 0);

• "education-num": peak at 10 and 13. These are the number of years of education.

• "hours-per-week" peaks at 40, this was very likely the standard number of working hours at the time of the data collection;

• most values of "capital-gain" and "capital-loss" are close to zero.

Inspecting categorical columns

For categorical variables, we can look at the distribution of values:

• We should do this for both the target variable and the input variables

adult_census[target_column].value_counts()

class
<=50K    37155
>50K     11687
Name: count, dtype: int64

Class imbalance

Imbalance in the target variable

• Classes are slightly imbalanced, meaning there are more samples of one or more classes compared to others.

• In this case, we have many more samples with " <=50K" than with " >50K".

• Class imbalance in the target variable happens often in practice and may need special techniques when building a predictive model.

• For example in a medical setting, if we are trying to predict whether subjects may develop a rare disease, there would be a lot more healthy subjects than ill subjects in the dataset.

Imbalance in the input data

adult_census["sex"].value_counts()

sex
Male      32650
Female    16192
Name: count, dtype: int64

• The data collection process led to an important imbalance between the number of male/female samples. Thus, our data are not representative of the US population.

• Training a model with such data imbalance can cause disproportioned prediction errors for the under-represented groups.

• This is a typical cause of fairness problems if used naively when deploying a machine learning based system in a real life setting.

Inspecting relationships between columns

In pandas

• We can use the crosstabulation feature from pandas to see how two variables are related

pd.crosstab(
    index=adult_census["education"], columns=adult_census["education-num"]
)

education-num	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
education
10th	0	0	0	0	0	1389	0	0	0	0	0	0	0	0	0	0
11th	0	0	0	0	0	0	1812	0	0	0	0	0	0	0	0	0
12th	0	0	0	0	0	0	0	657	0	0	0	0	0	0	0	0
1st-4th	0	247	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5th-6th	0	0	509	0	0	0	0	0	0	0	0	0	0	0	0	0
7th-8th	0	0	0	955	0	0	0	0	0	0	0	0	0	0	0	0
9th	0	0	0	0	756	0	0	0	0	0	0	0	0	0	0	0
Assoc-acdm	0	0	0	0	0	0	0	0	0	0	0	1601	0	0	0	0
Assoc-voc	0	0	0	0	0	0	0	0	0	0	2061	0	0	0	0	0
Bachelors	0	0	0	0	0	0	0	0	0	0	0	0	8025	0	0	0
Doctorate	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	594
HS-grad	0	0	0	0	0	0	0	0	15784	0	0	0	0	0	0	0
Masters	0	0	0	0	0	0	0	0	0	0	0	0	0	2657	0	0
Preschool	83	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Prof-school	0	0	0	0	0	0	0	0	0	0	0	0	0	0	834	0
Some-college	0	0	0	0	0	0	0	0	0	10878	0	0	0	0	0	0

Redundant columns

• For every entry in "education", there is only one single corresponding value in "education-num".

• This shows that "education" and "education-num" give you the same information.

• Thus, we can remove "education-num" without losing information.

• Note that having redundant (or highly correlated) columns can be a problem for machine learning algorithms.

We drop this column now and in all future notebooks.

adult_census = adult_census.drop(
    columns=["education"]
)  # duplicated in categorical column

Using pairplot

Another way to inspect the relationship between variables is to do a pairplot and show how each variable differs according to our target, i.e. "class". Plots along the diagonal show the distribution of individual variables for each "class". The plots on the off-diagonal can reveal interesting interactions between variables.

import seaborn as sns

# We plot a subset of the data to keep the plot readable and make the plotting
# faster
n_samples_to_plot = 5000
columns = ["age", "education-num", "hours-per-week"]
_ = sns.pairplot(
    data=adult_census[:n_samples_to_plot],
    vars=columns,
    hue=target_column,
    plot_kws={"alpha": 0.2},
    height=3,
    diag_kind="hist",
    diag_kws={"bins": 30},
)

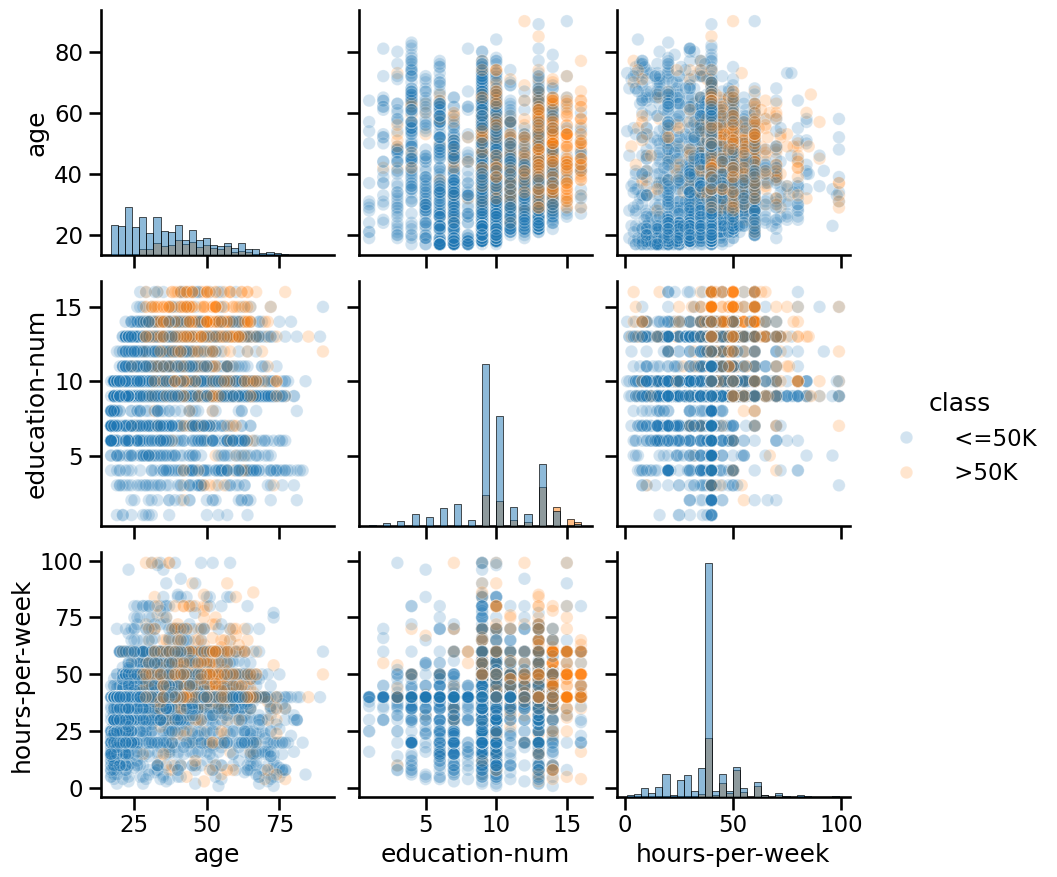
Notebook Recap

In this notebook we:

• looked at the different kind of variables to differentiate between categorical and numerical variables;

• inspected the data with pandas and seaborn. Data inspection can allow you to decide whether using machine learning is appropriate for your data and to highlight potential peculiarities in your data.

We made important observations (which will be discussed later in more detail):

• if your target variable is imbalanced (e.g., you have more samples from one target category than another), you may need special techniques for training and evaluating your machine learning model;

• having redundant (or highly correlated) columns can be a problem for some machine learning algorithms;

Sources

Data

We use data from the 1994 US census that we downloaded from OpenML.

You can look at the OpenML webpage to learn more about this dataset: http://www.openml.org/d/1590

Fairness in ML

We recommend our readers to refer to fairlearn.org for resources on how to quantify and potentially mitigate fairness issues related to the deployment of automated decision making systems that rely on machine learning components.