Content from introduction
Last updated on 2023-01-11 | Edit this page
Overview
Questions
- What problems are we solving, and what are we not discussing?
- Why do we use Python?
- What is parallel programming?
- Why can it be hard to write a parallel program?
Objectives
- Recognize serial and parallel patterns
- Identify problems that can be parallelized
- Understand a dependency diagram
Common problems
What problems are we solving?
Ask around what problems participants encountered: “Why did you sign up?”. Specifically: what is the domain science related task that you want to parallelize?
Most problems will fit in one of two categories: - I wrote this code in Python and it is not fast enough. - I run this code on my laptop, but the target problem size is bigger than the RAM.
In this course we will show several possible ways of speeding up your program and making it ready to function in parallel. We will be introducing the following modules:
-
threadingallows different parts of your program to run concurrently on a single computer (with shared memory) -
daskmakes scalable parallel computing easy -
numbaspeeds up your Python functions by translating them to optimized machine code -
memory_profilemonitors memory performance -
asyncioPython’s native asynchronous programming
FIXME: Actually explain functional programming & distributed programming More importantly, we will show how to change the design of a program to fit parallel paradigms. This often involves techniques from functional programming.
What we won’t talk about
In this course we will not talk about distributed programming. This is a huge can of worms. It is easy to show simple examples, but depending on the problem, solutions will be wildly different. Dask has a lot of functionality to help you in setting up for running on a network. The important bit is that, once you have made your code suitable for parallel computing, you’ll have the right mind-set to get it to work in a distributed environment.
Overview and rationale
FIXME: update this to newer lesson content organisation.
This is an advanced course. Why is it advanced? We (hopefully) saw in the discussion that although many of your problems share similar characteristics, it is the detail that will determine the solution. We all need our algorithms, models, analysis to run in a way that many hands make light work. When such a situation arises with a group of people, we start with a meeting discussing who does what, when do we meet again to sync up, etc. After a while you can get the feeling that all you do is be in meetings. We will see that there are several abstractions that can make our life easier. In large parts this course will use Dask to illustrate these abstractions.
- Vectorized instructions: tell many workers to do the same work on a
different piece of data. This is where
dask.arrayanddask.dataframecome in. We will illustrate this model of working by computing the number Pi later on. - Map/filter/reduce: this is a method where we combine different
functionals to create a larger program. We will use
dask.bagto count the number of unique words in a novel using this formalism. - Task-based parallelization: this may be the most generic abstraction
as all the others can be expressed in terms of tasks or workflows. This
is
dask.delayed.
Why Python?
Python is one of most widely used languages to do scientific data analysis, visualization, and even modelling and simulation. The popularity of Python is mainly due to the two pillars of a friendly syntax together with the availability of many high-quality libraries.
It’s not all good news
The flexibility that Python offers comes with a few downsides though: - Python code typically doesn’t perform as fast as lower-level implementations in C/C++ or Fortran. - It is not trivial to parallelize Python code to work efficiently on many-core architectures.
This workshop addresses both these issues, with an emphasis on being able to run Python code efficiently (in parallel) on multiple cores.
What is parallel computing?
Dependency diagrams
Suppose we have a computation where each step depends on a previous one. We can represent this situation like in the figure below, known as a dependency diagram:

In these diagrams the inputs and outputs of each function are represented as rectangles. The inward and outward arrows indicate their flow. Note that the output of one function can become the input of another one. The diagram above is the typical diagram of a serial computation. If you ever used a loop to update a value, you used serial computation.
If our computation involves independent work (that is, the results of the application of each function are independent of the results of the application of the rest), we can structure our computation like this:
This scheme corresponds to a parallel computation.
How can parallel computing improve our code execution speed?
Nowadays, most personal computers have 4 or 8 processors (also known as cores). In the diagram above, we can assign each of the three functions to one core, so they can be performed simultaneously.
Do 8 processors work 8 times faster than one?
It may be tempting to think that using eight cores instead of one would multiply the execution speed by eight. For now, it’s ok to use this a first approximation to reality. Later in the course we’ll see that things are actually more complicated than that.
Parallelizable and non-parallelizable tasks
Some tasks are easily parallelizable while others inherently aren’t. However, it might not always be immediately apparent that a task is parallelizable.
Let us consider the following piece of code.
PYTHON
x = [1, 2, 3, 4] # Write input
y = 0 # Initialize output
for i in range(len(x)):
y += x[i] # Add each element to the output variable
print(y) # Print outputOUTPUT
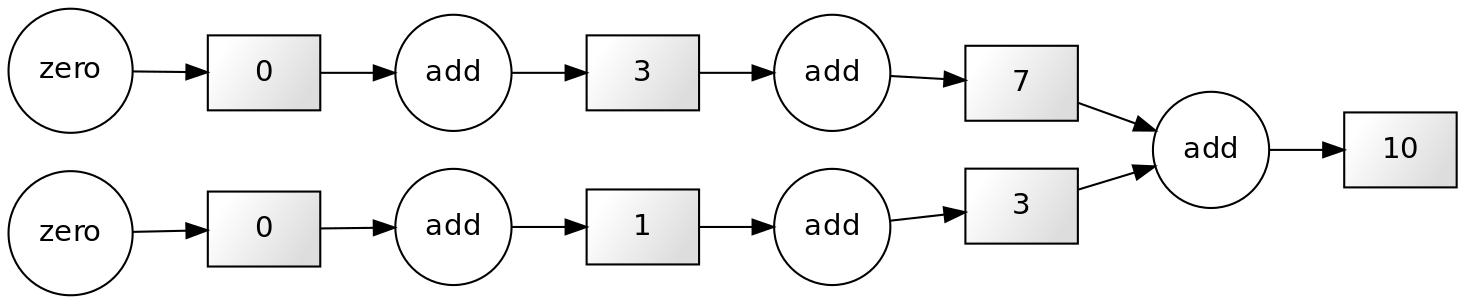
10Note that each successive loop uses the result of the previous loop. In that way, it is dependent on the previous loop. The following dependency diagram makes that clear:
Although we are performing the loops in a serial way in the snippet above, nothing avoids us from performing this calculation in parallel. The following example shows that parts of the computations can be done independently:
PYTHON
x = [1, 2, 4, 4]
chunk1 = x[:2]
chunk2 = x[2:]
sum_1 = sum(chunk1)
sum_2 = sum(chunk2)
result = sum_1 + sum_2
print(result)OUTPUT
10The technique for parallelising sums like this is called chunking.
There is a subclass of algorithms where the subtasks are completely independent. These kinds of algorithms are known as embarrassingly parallel, or more friendly: naturally or delightfully parallel.
An example of this kind of problem is squaring each element in a list, which can be done like so:
Each task of squaring a number is independent of all the other elements in the list.
It is important to know that some tasks are fundamentally
non-parallelizable. An example of such an inherently
serial algorithm could be the computation of the fibonacci
sequence using the formula Fn=Fn-1 + Fn-2. Each output here
depends on the outputs of the two previous loops.
Challenge: Parallellizable and non-parallellizable tasks
Can you think of a task in your domain that is parallelizable? Can you also think of one that is fundamentally non-parallelizable?
Please write your answers in the collaborative document.
Answers may differ. An ubiquitous example of a naturally parallel problem is a parameter scan, where you need to evaluate some model for N different configurations of input parameters.
One set of problems that are very hard to parallelize are solving time-dependent models where every state depends on the previous one. Even in those cases there are attempts to do parallel computation, but those require fundamentally different algorithms to solve.
In many cases fully paralellizable algorithms may be a bit less efficient per CPU cycle than their single threaded brethren.
Problems versus Algorithms
Often, the parallelizability of a problem depends on its specific implementation. For instance, in our first example of a non-parallelizable task, we mentioned the calculation of the Fibonacci sequence. However, there exists a closed form expression to compute the n-th Fibonacci number.
Last but not least, don’t let the name demotivate you: if your algorithm happens to be embarrassingly parallel, that’s good news! The “embarrassingly” refers to the feeling of “this is great!, how did I not notice before?!”
Challenge: Parallelised Pea Soup
We have the following recipe:
- (1 min) Pour water into a soup pan, add the split peas and bay leaf and bring it to boil.
- (60 min) Remove any foam using a skimmer and let it simmer under a lid for about 60 minutes.
- (15 min) Clean and chop the leek, celeriac, onion, carrot and potato.
- (20 min) Remove the bay leaf, add the vegetables and simmer for 20 more minutes. Stir the soup occasionally.
- (1 day) Leave the soup for one day. Reheat before serving and add a sliced smoked sausage (vegetarian options are also welcome). Season with pepper and salt.
Imagine you’re cooking alone.
- Can you identify potential for parallelisation in this recipe?
- And what if you are cooking with the help of a friend help? Is the soup done any faster?
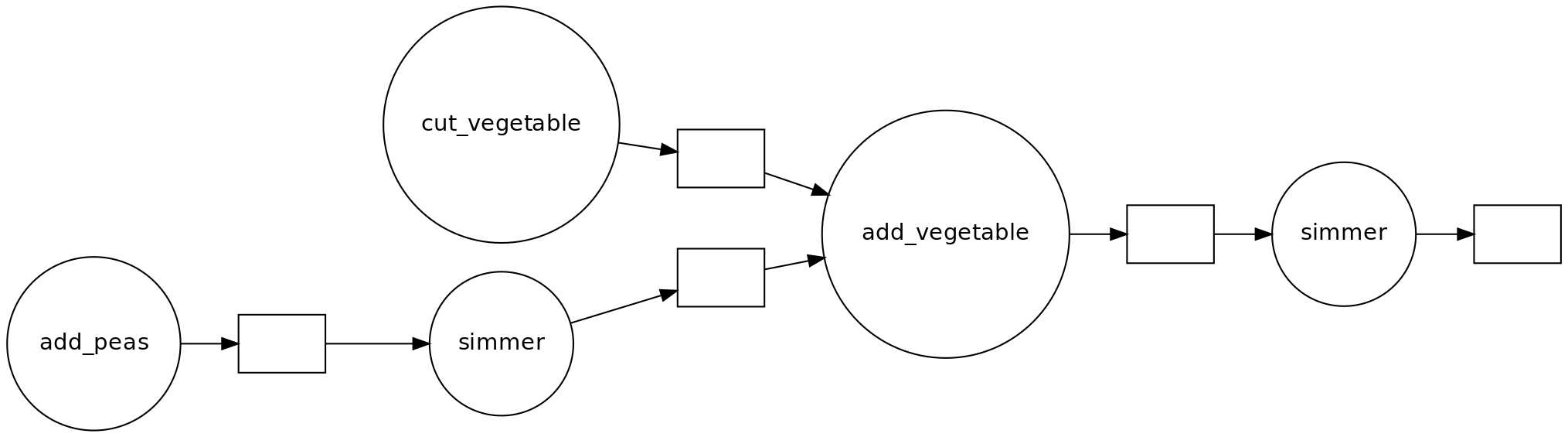
- Draw a dependency diagram.
- You can cut vegetables while simmering the split peas.
- If you have help, you can parallelize cutting vegetables further.
- There are two ‘workers’: the cook and the stove.
Shared vs. Distributed memory
FIXME: add text
Key Points
- Programs are parallelizable if you can identify independent tasks.
- To make programs scalable, you need to chunk the work.
- Parallel programming often triggers a redesign; we use different patterns.
- Doing work in parallel does not always give a speed-up.
Content from Benchmarking
Last updated on 2024-10-30 | Edit this page
Overview
Questions
- How do we know our program ran faster?
- How do we learn about efficiency?
Objectives
- View performance on system monitor
- Find out how many cores your machine has
- Use
%timeand%timeitline-magic - Use a memory profiler
- Plot performance against number of work units
- Understand the influence of hyper-threading on timings
A first example with Dask
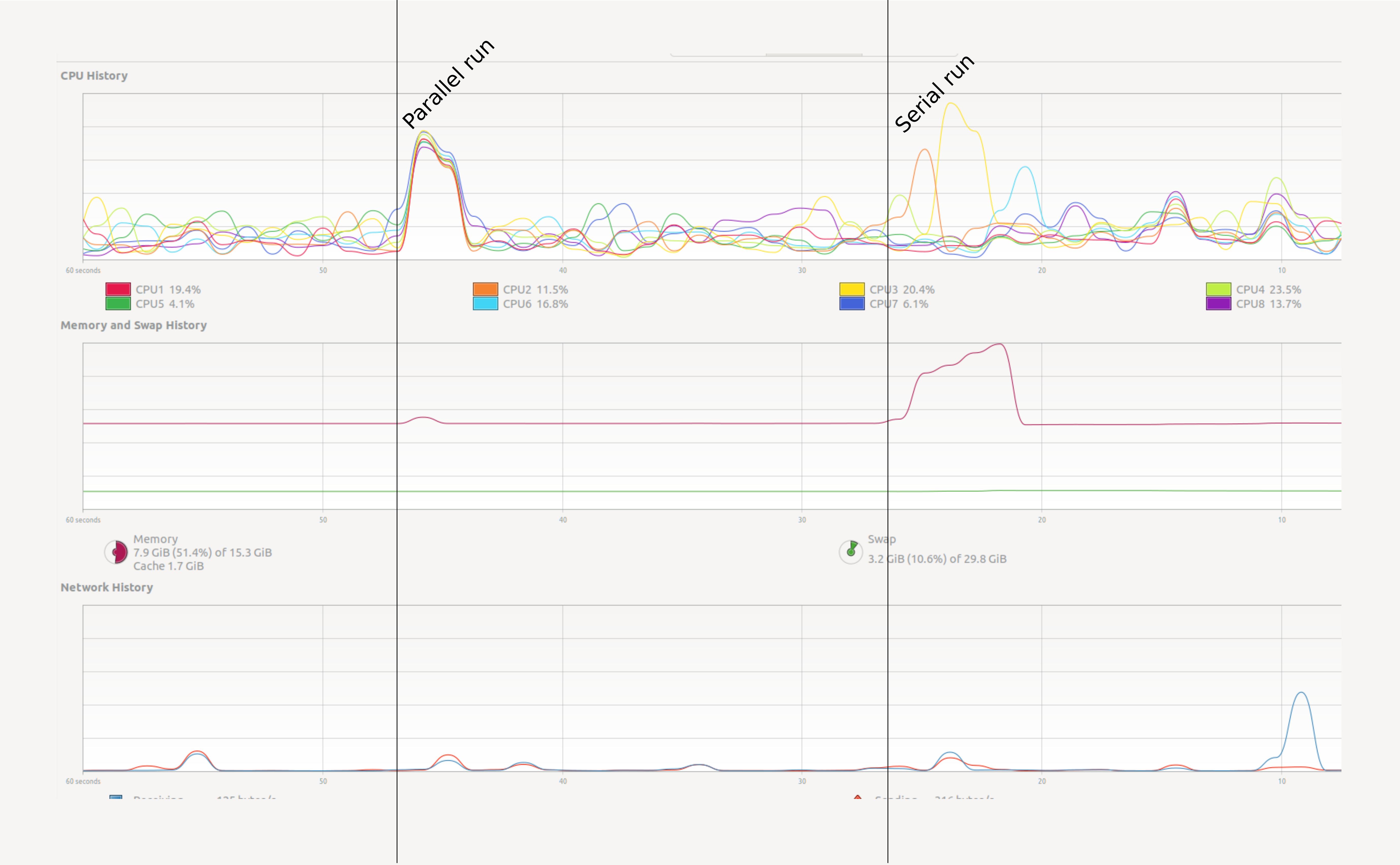
We will get into creating parallel programs in Python later. First let’s see a small example. Open your system monitor (this will differ among specific operating systems), and run the following code examples.
PYTHON
# The same summation, but using dask to parallelize the code.
# NB: the API for dask arrays mimics that of numpy
import dask.array as da
work = da.arange(10**7).sum()
result = work.compute()Try a heavy enough task
It could be that a task this small does not register on your radar.
Depending on your computer you will have to raise the power to
10**8 or 10**9 to make sure that it runs long
enough to observe the effect. But be careful and increase slowly. Asking
for too much memory can make your computer slow to a crawl.
How can we test this in a more practical way? In Jupyter we can use
some line magics, small “magic words” preceded by the symbol
%% that modify the behaviour of the cell.
The %%time line magic checks how long it took for a
computation to finish. It does nothing to change the computation itself.
In this it is very similar to the time shell command.
If run the chunk several times, we will notice a difference in the
times. How can we trust this timer, then? A possible solution will be to
time the chunk several times, and take the average time as our valid
measure. The %%timeit line magic does exactly this in a
concise an comfortable manner! %%timeit first measures how
long it takes to run a command one time, then repeats it enough times to
get an average run-time. Also, %%timeit can measure run
times without the time it takes to setup a problem, measuring only the
performance of the code in the cell. This way we can trust the outcome
better.
If you want to store the output of %%timeit in a Python
variable, you can do so with the -o flag.
Note that this does not tell you anything about memory consumption or efficiency.
Python’s map function is lazy. It won’t compute anything
until you iterate it. Try list(map(...)). The third example
doesn’t allocate any memory, which makes it faster.
Memory profiling
- The act of systematically testing performance under different conditions is called benchmarking.
- Analysing what parts of a program contribute to the total performance, and identifying possible bottlenecks is profiling.
We will use the memory_profiler
package to track memory usage. It can be installed executing the
code below in the console:
In Jupyter, type the following lines to compare the memory usage of
the serial and parallel versions of the code presented above (again,
change the value of 10**7 to something higher if
needed):
PYTHON
import numpy as np
import dask.array as da
from memory_profiler import memory_usage
import matplotlib.pyplot as plt
def sum_with_numpy():
# Serial implementation
np.arange(10**7).sum()
def sum_with_dask():
# Parallel implementation
work = da.arange(10**7).sum()
work.compute()
memory_numpy = memory_usage(sum_with_numpy, interval=0.01)
memory_dask = memory_usage(sum_with_dask, interval=0.01)
# Plot results
plt.plot(memory_numpy, label='numpy')
plt.plot(memory_dask, label='dask')
plt.xlabel('Time step')
plt.ylabel('Memory / MB')
plt.legend()
plt.show()The figure should be similar to the one below:
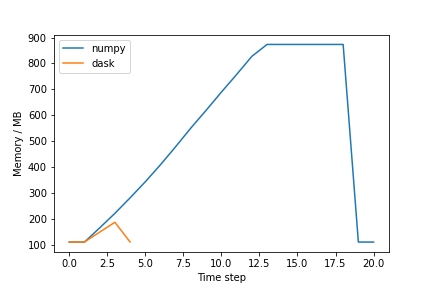
Exercise (plenary)
Why is the Dask solution more memory efficient?
Chunking! Dask chunks the large array, such that the data is never entirely in memory.
Profiling from Dask
Dask has several option to do profiling from Dask itself. See the dask documentation for more information.
Using many cores
Using more cores for a computation can decrease the run time. The first question is of course: how many cores do I have? See the snippets below to find out:
Find out how many cores your machine has
Usually the number of logical cores is higher than the number of physical course. This is due to hyper-threading, which enables each physical CPU core to execute several threads at the same time. Even with simple examples, performance may scale unexpectedly. There are many reasons for this, hyper-threading being one of them.
See for instance the example below:
On a machine with 4 physical and 8 logical cores doing this (admittedly oversimplistic) benchmark:
PYTHON
x = []
for n in range(1, 9):
time_taken = %timeit -r 1 -o da.arange(5*10**7).sum().compute(num_workers=n)
x.append(time_taken.average)Gives the following result:
PYTHON
import pandas as pd
data = pd.DataFrame({"n": range(1, 9), "t": x})
data.set_index("n").plot()Discussion
Why is the runtime increasing if we add more than 4 cores? This has to do with hyper-threading. On most architectures it does not make much sense to use more workers than the number of physical cores you have.
Key Points
- It is often non-trivial to understand performance
- Memory is just as important as speed
- Measuring is knowing
Content from Computing $\pi$
Last updated on 2023-01-04 | Edit this page
Overview
Questions
- How do I parallelize a Python application?
- What is data parallelism?
- What is task parallelism?
Objectives
- Rewrite a program in a vectorized form.
- Understand the difference between data and task-based parallel programming.
- Apply
numba.jitto accelerate Python.
Parallelizing a Python application
In order to recognize the advantages of parallelization we need an algorithm that is easy to parallelize, but still complex enough to take a few seconds of CPU time. To not scare away the interested reader, we need this algorithm to be understandable and, if possible, also interesting. We chose a classical algorithm for demonstrating parallel programming: estimating the value of number π.
The algorithm we present is one of the classical examples of the power of Monte-Carlo methods. This is an umbrella term for several algorithms that use random numbers to approximate exact results. We chose this algorithm because of its simplicity and straightforward geometrical interpretation.
We can compute the value of π using a random number generator. We count the points falling inside the blue circle M compared to the green square N. Then π is approximated by the ratio 4M/N.
Challenge: Implement the algorithm
PYTHON
import random
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / N
%timeit calc_pi(10**6)OUTPUT
676 ms ± 6.39 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)Before we start to parallelize this program, we need to do our best
to make the inner function as efficient as we can. We show two
techniques for doing this: vectorization using
numpy and native code generation using
numba.
We first demonstrate a Numpy version of this algorithm.
PYTHON
import numpy as np
def calc_pi_numpy(N):
# Simulate impact coordinates
pts = np.random.uniform(-1, 1, (2, N))
# Count number of impacts inside the circle
M = np.count_nonzero((pts**2).sum(axis=0) < 1)
return 4 * M / NThis is a vectorized version of the original algorithm. It nicely demonstrates data parallelization, where a single operation is replicated over collections of data. It contrasts to task parallelization, where different independent procedures are performed in parallel (think for example about cutting the vegetables while simmering the split peas).
If we compare with the ‘naive’ implementation above, we see that our new one is much faster:
OUTPUT
25.2 ms ± 1.54 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)Discussion: is this all better?
What is the downside of the vectorized implementation? - It uses more memory - It is less intuitive - It is a more monolithic approach, i.e. you cannot break it up in several parts
Challenge: Daskify
Write calc_pi_dask to make the Numpy version parallel.
Compare speed and memory performance with the Numpy version. NB:
Remember that dask.array mimics the numpy API.
PYTHON
import dask.array as da
def calc_pi_dask(N):
# Simulate impact coordinates
pts = da.random.uniform(-1, 1, (2, N))
# Count number of impacts inside the circle
M = da.count_nonzero((pts**2).sum(axis=0) < 1)
return 4 * M / N
%timeit calc_pi_dask(10**6).compute()OUTPUT
4.68 ms ± 135 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Using Numba to accelerate Python code
Numba makes it easier to create accelerated functions. You can use it
with the decorator numba.jit.
PYTHON
import numba
@numba.jit
def sum_range_numba(a):
"""Compute the sum of the numbers in the range [0, a)."""
x = 0
for i in range(a):
x += i
return xLet’s time three versions of the same test. First, native Python iterators:
OUTPUT
190 ms ± 3.26 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)Now with Numpy:
OUTPUT
17.5 ms ± 138 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)And with Numba:
OUTPUT
162 ns ± 0.885 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)Numba is 100x faster in this case! It gets this speedup with
“just-in-time” compilation (JIT)—compiling the Python function into
machine code just before it is called (that’s what the
@numba.jit decorator stands for). Not every Python and
Numpy feature is supported, but a function may be a good candidate for
Numba if it is written with a Python for-loop over a large range of
values, as with sum_range_numba().
Just-in-time compilation speedup
The first time you call a function decorated with
@numba.jit, you may see little or no speedup. In subsequent
calls, the function could be much faster. You may also see this warning
when using timeit:
The slowest run took 14.83 times longer than the fastest. This could mean that an intermediate result is being cached.
Why does this happen? On the first call, the JIT compiler needs to compile the function. On subsequent calls, it reuses the already-compiled function. The compiled function can only be reused if it is called with the same argument types (int, float, etc.).
See this example where sum_range_numba is timed again,
but now with a float argument instead of int:
OUTPUT
CPU times: user 58.3 ms, sys: 3.27 ms, total: 61.6 ms
Wall time: 60.9 ms
CPU times: user 5 µs, sys: 0 ns, total: 5 µs
Wall time: 7.87 µsChallenge: Numbify calc_pi
Create a Numba version of calc_pi. Time it.
Add the @numba.jit decorator to the first ‘naive’
implementation.
PYTHON
@numba.jit
def calc_pi_numba(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / N
%timeit calc_pi_numba(10**6)OUTPUT
13.5 ms ± 634 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)Measuring == knowing
Always profile your code to see which parallelization method works best.
numba.jit is not a magical
command to solve are your problems
Using numba to accelerate your code often outperforms other methods, but it is not always trivial to rewrite your code so that you can use numba with it.
Key Points
- Always profile your code to see which parallelization method works best
- Vectorized algorithms are both a blessing and a curse.
- Numba can help you speed up code
Content from Threads and processes
Last updated on 2023-01-06 | Edit this page
Overview
Questions
- What is the Global Interpreter Lock (GIL)?
- How do I use multiple threads in Python?
Objectives
- Understand the GIL.
- Understand the difference between the python
threadingandmultiprocessinglibrary
Threading
Another possibility for parallelization is to use the
threading module. This module is built into Python. In this
section, we’ll use it to estimate pi once again.
Using threading to speed up your code:
PYTHON
%%time
n = 10**7
t1 = Thread(target=calc_pi, args=(n,))
t2 = Thread(target=calc_pi, args=(n,))
t1.start()
t2.start()
t1.join()
t2.join()Discussion: where’s the speed-up?
While mileage may vary, parallelizing calc_pi,
calc_pi_numpy and calc_pi_numba this way will
not give the expected speed-up. calc_pi_numba should give
some speed-up, but nowhere near the ideal scaling over the
number of cores. This is because Python only allows one thread to access
the interperter at any given time, a feature also known as the Global
Interpreter Lock.
A few words about the Global Interpreter Lock
The Global Interpreter Lock (GIL) is an infamous feature of the Python interpreter. It both guarantees inner thread sanity, making programming in Python safer, and prevents us from using multiple cores from a single Python instance. When we want to perform parallel computations, this becomes an obvious problem. There are roughly two classes of solutions to circumvent/lift the GIL:
- Run multiple Python instances:
multiprocessing - Have important code outside Python: OS operations, C++ extensions, cython, numba
The downside of running multiple Python instances is that we need to
share program state between different processes. To this end, you need
to serialize objects. Serialization entails converting a Python object
into a stream of bytes, that can then be sent to the other process, or
e.g. stored to disk. This is typically done using pickle,
json, or similar, and creates a large overhead. The
alternative is to bring parts of our code outside Python. Numpy has many
routines that are largely situated outside of the GIL. The only way to
know for sure is trying out and profiling your application.
To write your own routines that do not live under the GIL there are
several options: fortunately numba makes this very
easy.
We can force the GIL off in Numba code by setting
nogil=True in the numba.jit decorator.
PYTHON
@numba.jit(nopython=True, nogil=True)
def calc_pi_nogil(N):
M = 0
for i in range(N):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x**2 + y**2 < 1:
M += 1
return 4 * M / NThe nopython argument forces Numba to compile the code
without referencing any Python objects, while the nogil
argument enables lifting the GIL during the execution of the
function.
Use nopython=True or
@numba.njit
It’s generally a good idea to use nopython=True with
@numba.jit to make sure the entire function is running
without referencing Python objects, because that will dramatically slow
down most Numba code. There’s even a decorator that has
nopython=True by default: @numba.njit
Now we can run the benchmark again, using calc_pi_nogil
instead of calc_pi.
Exercise: try threading on a Numpy function
Many Numpy functions unlock the GIL. Try to sort two randomly
generated arrays using numpy.sort in parallel.
Multiprocessing
Python also allows for using multiple processes for parallelisation
via the multiprocessing module. It implements an API that
is superficially similar to threading:
PYTHON
from multiprocessing import Process
def calc_pi(N):
...
if __name__ == '__main__':
n = 10**7
p1 = Process(target=calc_pi, args=(n,))
p2 = Process(target=calc_pi, args=(n,))
p1.start()
p2.start()
p1.join()
p2.join()However under the hood processes are very different from threads. A new process is created by creating a fresh “copy” of the python interpreter, that includes all the resources associated to the parent. There are three different ways of doing this (spawn, fork, and forkserver), which depends on the platform. We will use spawn as it is available on all platforms, you can read more about the others in the Python documentation. As creating a process is resource intensive, multiprocessing is beneficial under limited circumstances - namely, when the resource utilisation (or runtime) of a function is measureably larger than the overhead of creating a new process.
The non-intrusive and safe way of starting a new process is acquire a
context, and working within the context. This ensures your
application does not interfere with any other processes that might be in
use.
PYTHON
import multiprocessing as mp
def calc_pi(N):
...
if __name__ == '__main__':
# mp.set_start_method("spawn") # if not using a context
ctx = mp.get_context("spawn")
...Passing objects and sharing state
We can pass objects between processes by using Queues
and Pipes. Multiprocessing queues behave similarly to
regular queues: - FIFO: first in, first out -
queue_instance.put(<obj>) to add -
queue_instance.get() to retrieve
Exercise: reimplement calc_pi to
use a queue to return the result
PYTHON
import multiprocessing as mp
import random
def calc_pi(N, que):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
que.put((4 * M / N, N)) # result, iterations
if __name__ == "__main__":
ctx = mp.get_context("spawn")
que = ctx.Queue()
n = 10**7
p1 = ctx.Process(target=calc_pi, args=(n, que))
p2 = ctx.Process(target=calc_pi, args=(n, que))
p1.start()
p2.start()
for i in range(2):
print(que.get())
p1.join()
p2.join()Process pool
The Pool API provides a pool of worker processes that
can execute tasks. Methods of the pool object offer various convenient
ways to implement data parallelism in your program. The most convenient
way to create a pool object is with a context manager, either using the
toplevel function multiprocessing.Pool, or by calling the
.Pool() method on the context. With the pool object, tasks
can be submitted by calling methods like .apply(),
.map(), .starmap(), or their
.*_async() versions.
Exercise: adapt the original exercise to submit tasks to a pool
- Use the original
calc_pifunction (without the queue) - Submit batches of different sample size (different values of
N). - As mentioned earlier, creating a new process has overhead. Try a wide range of sample sizes and check if runtime scaling supports that claim.
PYTHON
from itertools import repeat
import multiprocessing as mp
import random
from timeit import timeit
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return (4 * M / N, N) # result, iterations
def submit(ctx, N):
with ctx.Pool() as pool:
pool.starmap(calc_pi, repeat((N,), 4))
if __name__ == "__main__":
ctx = mp.get_context("spawn")
for i in (1_000, 100_000, 10_000_000):
res = timeit(lambda: submit(ctx, i), number=5)
print(i, res)Key Points
- If we want the most efficient parallelism on a single machine, we need to circumvent the GIL.
- If your code releases the GIL, threading will be more efficient than multiprocessing.
- If your code does not release the GIL, some of your code is still in Python, and you’re wasting precious compute time!
Content from Delayed evaluation
Last updated on 2023-01-06 | Edit this page
Overview
Questions
- What abstractions does Dask offer?
- How can I paralellize existing Python code?
Objectives
- Understand the abstraction of delayed evaluation
- Use the
visualizemethod to create dependency graphs
Dask is one of the many tools
available for parallelizing Python code in a comfortable way. We’ve seen
a basic example of dask.array in a previous episode. Now,
we will focus on the delayed and bag
sub-modules. Dask has a lot of other useful components, such as
dataframe and futures, but we are not going to
cover them in this lesson.
See an overview below:
| Dask module | Abstraction | Keywords | Covered |
|---|---|---|---|
dask.array |
numpy |
Numerical analysis | ✔️ |
dask.bag |
itertools |
Map-reduce, workflows | ✔️ |
dask.delayed |
functions | Anything that doesn’t fit the above | ✔️ |
dask.dataframe |
pandas |
Generic data analysis | ❌ |
dask.futures |
concurrent.futures |
Control execution, low-level | ❌ |
Dask Delayed
A lot of the functionality in Dask is based on top of a concept known
as delayed evaluation. Because this concept is so very
important in understanding how Dask functions, we will go a bit deeper
into dask.delayed.
By using dask.delayed we change the strategy by which
our computation is evaluated. Normally in a computer, you expect
commands to be run when you ask for them, and then when the job is
complete, you can give the next command. When we use delayed evaluation,
we don’t wait around to formulate the next command. Instead we create
the dependency graph of our complete computation without actually doing
any work. When we know the full dependency graph, we can see which jobs
can be done in parallel and give those to different workers.
To express a computation in this world, we need to handle future objects as if they’re already there. These objects may be refered to as futures or promises.
Callout
Python has support for working with futures in several libraries, each time slightly different. The main difference between Python futures and Dask delayed objects is that futures are added to a queue from the first moment you define them, while delayed objects are silent until you ask to compute. We will refer to these ‘live’ futures as futures, and ‘dead’ futures (like delayed) as promises.
The delayed decorator builds a dependency graph from
function calls.
A delayed function stores the requested function call
inside a promise. The function is not actually executed
yet, instead we are promised a value that can be computed
later.
We can check that x_p is now a Delayed
value.
OUTPUT
[out]: dask.delayed.DelayedNote
It is often a good idea to suffix variables that you know are promises with
_p. That way you keep track of promises versus immediate values. {: .callout}
Only when we evaluate the computation, do we get an output.
OUTPUT
1 + 2 = 3
[out]: 3From Delayed values we can create larger workflows and
visualize them.
Challenge: run the workflow
Given this workflow:
Visualize and compute y_p and z_p
separately, how often is x_p evaluated?
Now change the workflow:
We pass the yet uncomputed promise x_p to both
y_p and z_p. Now, only compute
z_p, how often do you expect x_p to be
evaluated? Run the workflow to check your answer.
We can also make a promise by directly calling
delayed
It is now possible to call visualize or
compute methods on x_p.
Decorators
In Python the decorator syntax is equivalent to passing a function through a function adapter (a.k.a. a higher order function or a functional). This adapter can change the behaviour of the function in many ways. The statement,
is functionally equivalent to:
We can build new primitives from the ground up. An important function
that you will find in many different places where non-standard
evaluation strategies are involved is gather. We can
implement gather as follows:
Challenge: understand gather
Can you describe what the gather function does in terms
of lists and promises? hint: Suppose I have a list of promises, what
does gather allow me to do?
It turns a list of promises into a promise of a list.
We can visualize what gather does by this small
example.
PYTHON
x_p = gather(*(add(n, n) for n in range(10))) # Shorthand for gather(add(1, 1), add(2, 2), ...)
x_p.visualize()
{.output alt=“boxes and arrows”}
Computing the result,
OUTPUT
[out]: [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]Challenge: design a mean function
and calculate pi
PYTHON
from dask import delayed
import random
@delayed
def mean(*args):
return sum(args) / len(args)
def calc_pi(N):
"""Computes the value of pi using N random samples."""
M = 0
for i in range(N):
# take a sample
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x*x + y*y < 1.: M+=1
return 4 * M / N
N = 10**6
pi_p = mean(*(delayed(calc_pi)(N) for i in range(10)))
pi_p.compute()You may not seed a significant speedup. This is because
dask delayed uses threads by default and our native Python
implementation of calc_pi does not circumvent the GIL. With
for example the numba version of calc_pi you should see a
more significant speedup.
In practice you may not need to use @delayed functions
too often, but it does offer ultimate flexibility. You can build complex
computational workflows in this manner, sometimes replacing shell
scripting, make files and the likes.
Key Points
- We can change the strategy by which a computation is evaluated.
- Nothing is computed until we run
compute(). - By using delayed evaluation, Dask knows which jobs can be run in parallel.
- Call
computeonly once at the end of your program to get the best results.
Content from Map and reduce
Last updated on 2023-01-11 | Edit this page
Overview
Questions
- What abstractions does Dask offer?
- What programming patterns exist in the parallel universe?
Objectives
- Recognize
map,filterandreducepatterns - Create programs using these building blocks
- Use the
visualizemethod to create dependency graphs
In computer science bags refer to unordered collections of
data. In Dask, a bag is a collection that is chunked
internally. When you perform operations on a bag, these operations are
automatically parallelized over the chunks inside the bag.
Dask bags let you compose functionality using several primitive
patterns: the most important of these are map,
filter, groupby, flatten, and
reduction.
Discussion
Open the Dask
documentation on bags. Discuss the map,
filter, flatten and reduction
methods
In this set of operations reduction is rather special.
All other operations on bags could be written in terms of a
reduction.
Operations on this level can be distinguished in several categories:
- map (N to N) applies a function one-to-one on a list of arguments. This operation is embarrassingly parallel.
- filter (N to <N) selects a subset from the data.
- reduce (N to 1) computes an aggregate from a sequence of data; if the operation permits it (summing, maximizing, etc) this can be done in parallel by reducing chunks of data and then further processing the results of those chunks.
- groupby (1 bag to N bags) groups data in subcategories.
- flatten (N bags to 1 bag) combine many bags into one.
Let’s see an example of it in action:
First, let’s create the bag containing the elements we
want to work with (in this case, the numbers from 0 to 5).
{: .source}
Map
To illustrate the concept of map, we’ll need a mapping
function. In the example below we’ll just use a function that squares
its argument:
PYTHON
# Create a function for mapping
def f(x):
return x.upper()
# Create the map and compute it
bag.map(f).compute()OUTPUT
out: ['MARY', 'HAD', 'A', 'LITTLE', 'LAMB']We can also visualize the mapping:
Filter
To illustrate the concept of filter, it is useful to
have a function that returns a boolean. In this case, we’ll use a
function that returns True if the argument contains the
letter ‘a’, and False if it doesn’t.
PYTHON
# Return True if x is even, False if not
def pred(x):
return 'a' in x
bag.filter(pred).compute()OUTPUT
[out]: ['mary', 'had', 'a', 'lamb']Difference between filter and
map
Without executing it, try to forecast what would be the output of
bag.map(pred).compute().
The output will be [True, True, True, False, True].
Reduction
PYTHON
def count_chars(x):
per_word = [len(w) for w in x]
return sum(per_word)
bag.reduction(count_chars, sum).visualize()Challenge: consider pluck
We previously discussed some generic operations on bags. In the
documentation, lookup the pluck method. How would you
implement this if pluck wasn’t there?
hint: Try pluck on some example data.
FIXME: find replacement for word counting example
Challenge: Dask version of Pi estimation
Use map and mean functions on Dask bags to
compute \(\pi\).
PYTHON
import dask.bag
from numpy import repeat
import random
def calc_pi(N):
"""Computes the value of pi using N random samples."""
M = 0
for i in range(N):
# take a sample
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x*x + y*y < 1.: M+=1
return 4 * M / N
bag = dask.bag.from_sequence(repeat(10**7, 24))
shots = bag.map(calc_pi)
estimate = shots.mean()
estimate.compute()Note
By default Dask runs a bag using multi-processing. This alleviates problems with the GIL, but also means a larger overhead.
Key Points
- Use abstractions to keep programs manageable
Content from Exercise with Fractals
Last updated on 2023-01-11 | Edit this page
Overview
Questions
- Can we try a real problem now?
Objectives
- Create a strategy to parallelise existing code
- Apply previous lessons
The Mandelbrot and Julia fractals
This exercise uses Numpy and Matplotlib.
We will be computing the famous Mandelbrot fractal.
Complex numbers
Complex numbers are a special representation of rotations and scalings in the two-dimensional plane. Multiplying two complex numbers is the same as taking a point, rotate it by an angle \(\phi\) and scale it by the absolute value. Multiplying with a number \(z \in \mathbb{C}\) by 1 preserves \(z\). Multiplying a point at \(i = (0, 1)\) (having a positive angle of 90 degrees and absolute value 1), rotates it anti-clockwise by 90 degrees. Then you might see that \(i^2 = (-1, 0)\). The funny thing is, that we can treat \(i\) as any ordinary number, and all our algebra still works out. This is actually nothing short of a miracle! We can write a complex number
\[z = x + iy,\]
remember that \(i^2 = -1\) and act as if everything is normal!
The Mandelbrot set is the set of complex numbers \[c \in \mathbb{C}\] for which the iteration,
\[z_{n+1} = z_n^2 + c,\]
converges, starting iteration at \(z_0 = 0\). We can visualize the Mandelbrot set by plotting the number of iterations needed for the absolute value \(|z_n|\) to exceed 2 (for which it can be shown that the iteration always diverges).
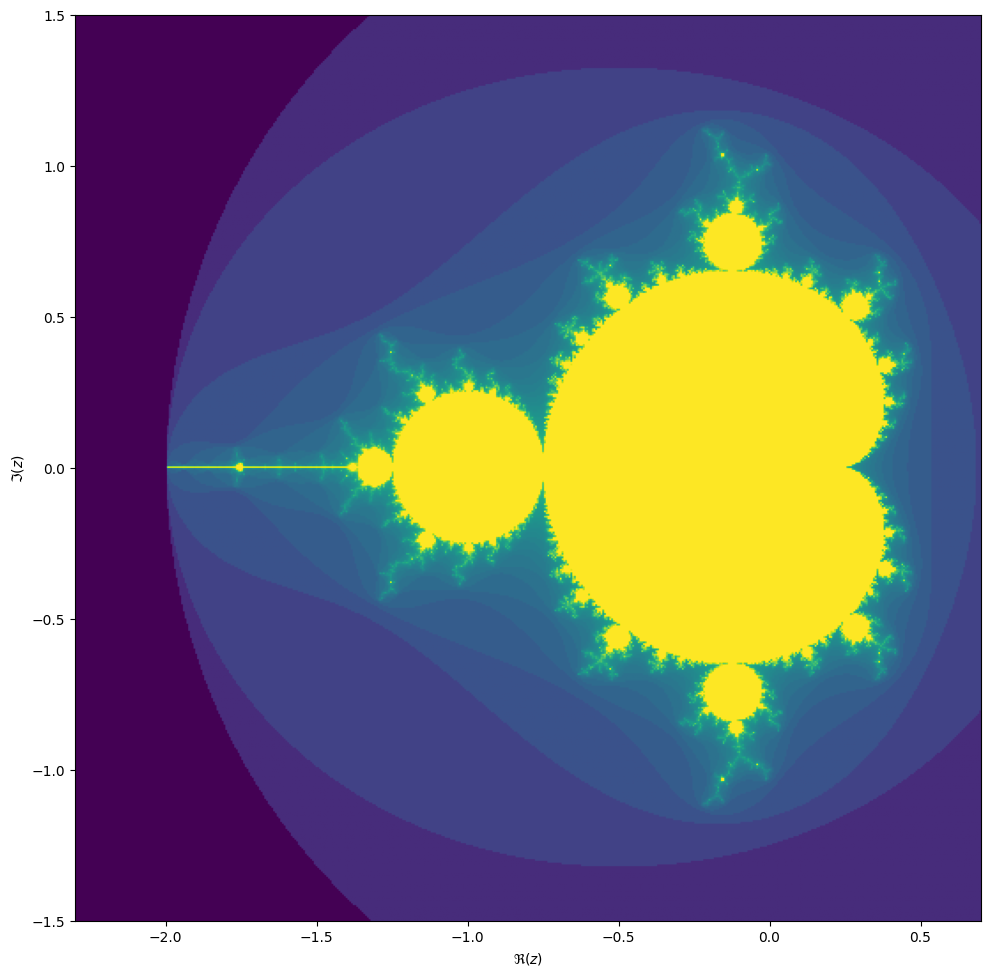
We may compute the Mandelbrot as follows:
PYTHON
max_iter = 256
width = 256
height = 256
center = -0.8+0.0j
extent = 3.0+3.0j
scale = max((extent / width).real, (extent / height).imag)
result = np.zeros((height, width), int)
for j in range(height):
for i in range(width):
c = center + (i - width // 2 + (j - height // 2)*1j) * scale
z = 0
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real > 4.0:
break
result[j, i] = kThen we can plot with the following code:
PYTHON
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
plot_extent = (width + 1j * height) * scale
z1 = center - plot_extent / 2
z2 = z1 + plot_extent
ax.imshow(result**(1/3), origin='lower', extent=(z1.real, z2.real, z1.imag, z2.imag))
ax.set_xlabel("$\Re(c)$")
ax.set_ylabel("$\Im(c)$")Things become really loads of fun when we start to zoom in. We can
play around with the center and extent values
(and necessarily max_iter) to control our window.
When we zoom in on the Mandelbrot fractal, we get smaller copies of the larger set!
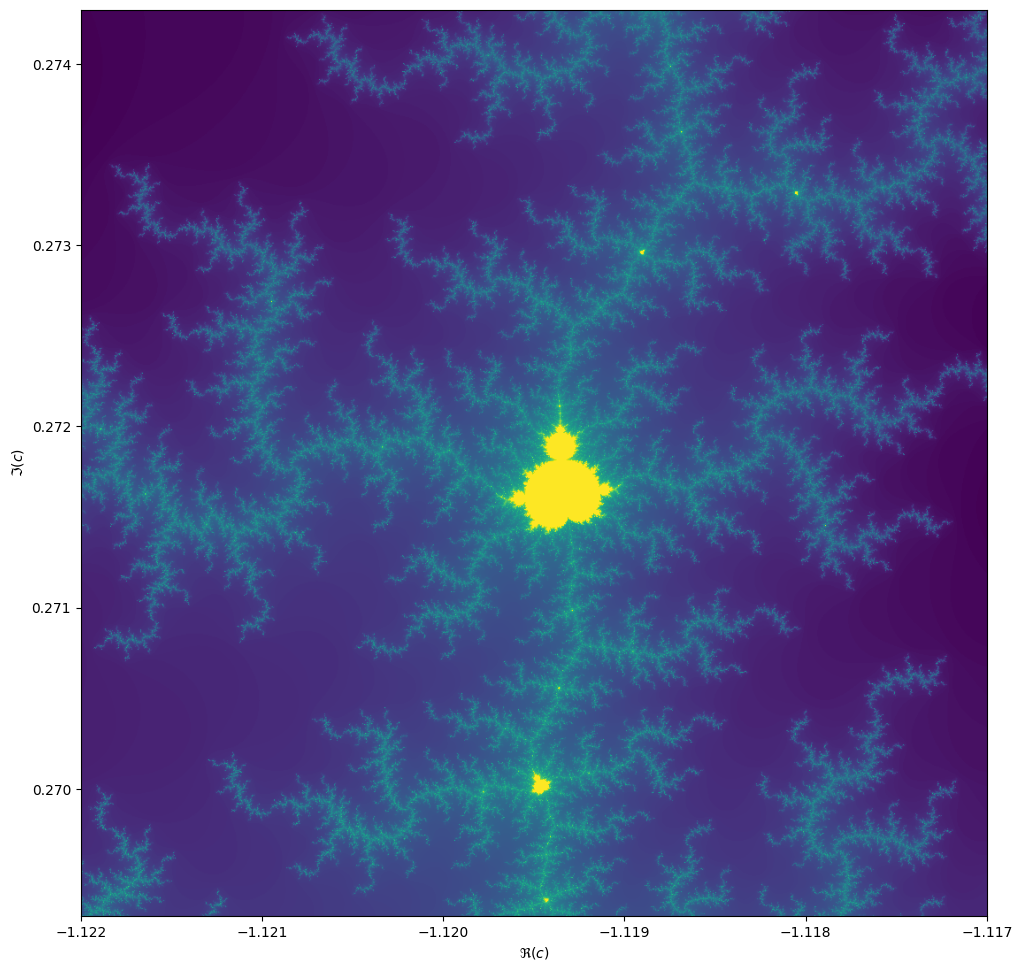
Exercise
Make this into an efficient parallel program. What kind of speed-ups do you get?
We start with a naive implementation. It may be convenient to define
a BoundingBox class in a separate module
bounding_box.py. We’ll add methods to this class later
on.
PYTHON
from dataclasses import dataclass
from typing import Optional
import numpy as np
import dask.array as da
@dataclass
class BoundingBox:
width: int
height: int
center: complex
extent: complex
_scale: Optional[float] = None
@property
def scale(self):
if self._scale is None:
self._scale = max(self.extent.real / self.width,
self.extent.imag / self.height)
return self._scale
<<bounding-box-methods>>
test_case = BoundingBox(1024, 1024, -1.1195+0.2718j, 0.005+0.005j)PYTHON
import matplotlib # type:ignore
matplotlib.use(backend="Agg")
from matplotlib import pyplot as plt
import numpy as np
from .bounding_box import BoundingBox
def plot_fractal(box: BoundingBox, values: np.ndarray, ax=None):
if ax is None:
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
else:
fig = None
plot_extent = (box.width + 1j * box.height) * box.scale
z1 = box.center - plot_extent / 2
z2 = z1 + plot_extent
ax.imshow(values, origin='lower', extent=(z1.real, z2.real, z1.imag, z2.imag),
cmap=matplotlib.colormaps["jet"])
ax.set_xlabel("$\Re(c)$")
ax.set_ylabel("$\Im(c)$")
return fig, axThe main approach with Python will be: use Numba to make this fast.
Then there are two ways to parallelize: let Numba parallelize the
function, or do a manual domain decomposition and use one of many ways
in Python to run things multi-threaded. There is a third way: create a
vectorized function and parallelize using dask.array. This
last option is almost always slower than
@njit(parallel=True) or domain decomposition.
PYTHON
When we port the core Mandelbrot function to Numba, we need to keep some best practices in mind:
- Don’t pass composite objects other than Numpy arrays.
- Avoid acquiring memory inside a Numba function; create an array in Python, then pass it to the Numba function.
- Write a Pythonic wrapper around the Numba function for easy use.
PYTHON
from typing import Any, Optional
import numba # type:ignore
import numpy as np
from .bounding_box import BoundingBox
@numba.njit(nogil=True)
def compute_mandelbrot_numba(
result, width: int, height: int, center: complex,
scale: complex, max_iter: int):
for j in range(height):
for i in range(width):
c = center + (i - width // 2 + (j - height // 2) * 1j) * scale
z = 0.0+0.0j
for k in range(max_iter):
z = z**2 + c
if (z*z.conjugate()).real >= 4.0:
break
result[j, i] = k
return result
def compute_mandelbrot(
box: BoundingBox, max_iter: int,
result: Optional[np.ndarray[np.int64]] = None,
throttle: Any = None):
result = result if result is not None \
else np.zeros((box.height, box.width), np.int64)
return compute_mandelbrot_numba(
result, box.width, box.height, box.center, box.scale,
max_iter=max_iter)Numba parallel=True
We can parallelize loops directly with Numba. Pass the flag
parallel=True and use prange to create the
loop. Here it is even more important to obtain the result array outside
the context of Numba, or the result will be slower than the serial
version.
PYTHON
from typing import Optional
import numba # type:ignore
from numba import prange # type:ignore
import numpy as np
from .bounding_box import BoundingBox
@numba.njit(nogil=True, parallel=True)
def compute_mandelbrot_numba(
result, width: int, height: int, center: complex, scale: complex,
max_iter: int):
for j in prange(height):
for i in prange(width):
c = center + (i - width // 2 + (j - height // 2) * 1j) * scale
z = 0.0+0.0j
for k in range(max_iter):
z = z**2 + c
if (z*z.conjugate()).real >= 4.0:
break
result[j, i] = k
return result
def compute_mandelbrot(box: BoundingBox, max_iter: int,
throttle: Optional[int] = None):
if throttle is not None:
numba.set_num_threads(throttle)
result = np.zeros((box.height, box.width), np.int64)
return compute_mandelbrot_numba(
result, box.width, box.height, box.center, box.scale,
max_iter=max_iter)We split the computation into a set of sub-domains. The
BoundingBox.split() method is designed such that if we
deep-map the resulting list-of-lists, we can recombine the results using
numpy.block().
PYTHON
def split(self, n):
"""Split the domain in nxn subdomains, and return a grid of BoundingBoxes."""
w = self.width // n
h = self.height // n
e = self.scale * w + self.scale * h * 1j
x0 = self.center - e * (n / 2 - 0.5)
return [[BoundingBox(w, h, x0 + i * e.real + j * e.imag * 1j, e)
for i in range(n)]
for j in range(n)]To perform the computation in parallel, lets go ahead and chose the
most difficult path: asyncio. There are other ways to do
this, setting up a number of threads, or use Dask. However,
asyncio is available to us in Python natively. In the end,
the result is very similar to what we would get using
dask.delayed.
This may seem as a lot of code, but remember: we only used Numba to compile the core part and then used Asyncio to parallelize. The progress bar is a bit of flutter and the semaphore is only there to throttle the computation to fewer cores. Even then, this solution is by far the most extensive, but also the fastest.
PYTHON
from typing import Optional
import numpy as np
import asyncio
from psutil import cpu_count # type:ignore
from contextlib import nullcontext
from .bounding_box import BoundingBox
from .numba_serial import compute_mandelbrot as mandelbrot_serial
async def a_compute_mandelbrot(
box: BoundingBox,
max_iter: int,
semaphore: Optional[asyncio.Semaphore]):
async with semaphore or nullcontext():
result = np.zeros((box.height, box.width), np.int64)
await asyncio.to_thread(
mandelbrot_serial, box, max_iter, result=result)
return result
async def a_domain_split(box: BoundingBox, max_iter: int,
sem: Optional[asyncio.Semaphore]):
n_cpus = cpu_count(logical=True)
split = box.split(n_cpus)
split_result = await asyncio.gather(
*(asyncio.gather(
*(a_compute_mandelbrot(b, max_iter, sem)
for b in row))
for row in split))
return np.block(split_result)
def compute_mandelbrot(box: BoundingBox, max_iter: int,
throttle: Optional[int] = None):
sem = asyncio.Semaphore(throttle) if throttle is not None else None
return asyncio.run(a_domain_split(box, max_iter, sem))Another solution is to use Numba’s @guvectorize
decorator. The speed-up (on my machine) is not as dramatic as with the
domain-decomposition though.
PYTHON
def grid(self):
"""Return the complex values on the grid in a 2d array."""
x0 = self.center - self.extent / 2
x1 = self.center + self.extent / 2
g = np.mgrid[x0.imag:x1.imag:self.height*1j,
x0.real:x1.real:self.width*1j]
return g[1] + g[0]*1j
def da_grid(self):
"""Return the complex values on the grid in a 2d array."""
x0 = self.center - self.extent / 2
x1 = self.center + self.extent / 2
x = np.linspace(x0.real, x1.real, self.width, endpoint=False)
y = np.linspace(x0.imag, x1.imag, self.height, endpoint=False)
g = da.meshgrid(x, y)
return g[1] + g[0]*1jPYTHON
from typing import Any
from numba import guvectorize, int64, complex128 # type:ignore
import numpy as np
from .bounding_box import BoundingBox
@guvectorize([(complex128[:, :], int64, int64[:, :])],
"(n,m),()->(n,m)",
nopython=True)
def compute_mandelbrot_numba(inp, max_iter: int, result):
for j in range(inp.shape[0]):
for i in range(inp.shape[1]):
c = inp[j, i]
z = 0.0+0.0j
for k in range(max_iter):
z = z**2 + c
if (z*z.conjugate()).real >= 4.0:
break
result[j, i] = k
def compute_mandelbrot(box: BoundingBox, max_iter: int, throttle: Any = None):
result = np.zeros((box.height, box.width), np.int64)
c = box.grid()
compute_mandelbrot_numba(c, max_iter, result)
return resultPYTHON
from typing import Optional
import timeit
from . import numba_serial, numba_parallel, vectorized, domain_splitting
from .bounding_box import BoundingBox, test_case
compile_box = BoundingBox(16, 16, 0.0+0.0j, 1.0+1.0j)
timing_box = test_case
def compile_run(m):
m.compute_mandelbrot(compile_box, 1)
def timing_run(m, throttle: Optional[int] = None):
m.compute_mandelbrot(timing_box, 1024, throttle=throttle)
modules = ["numba_serial:1", "vectorized:1"] \
+ [f"domain_splitting:{n}" for n in range(1, 9)] \
+ [f"numba_parallel:{n}" for n in range(1, 9)]
if __name__ == "__main__":
with open("timings.txt", "w") as out:
headings = ["name", "n", "min", "mean", "max"]
print(f"{headings[0]:<20}" \
f"{headings[1]:>10}" \
f"{headings[2]:>10}" \
f"{headings[3]:>10}" \
f"{headings[4]:>10}",
file=out)
for mn in modules:
m, n = mn.split(":")
n_cpus = int(n)
setup = f"from mandelbrot.bench_all import timing_run, compile_run\n" \
f"from mandelbrot import {m}\n" \
f"compile_run({m})"
times = timeit.repeat(
stmt=f"timing_run({m}, {n_cpus})",
setup=setup,
number=1,
repeat=50)
print(f"{m:20}" \
f"{n_cpus:>10}" \
f"{min(times):10.5g}" \
f"{sum(times)/len(times):10.5g}" \
f"{max(times):10.5g}",
file=out)
import pandas as pd
from plotnine import ggplot, geom_point, geom_ribbon, geom_line, aes
timings = pd.read_table("timings.txt", delimiter=" +", engine="python")
plot = ggplot(timings, aes(x="n", y="mean", ymin="min", ymax="max",
color="name", fill="name")) \
+ geom_ribbon(alpha=0.3, color="none") \
+ geom_point() + geom_line()
plot.save("mandelbrot-timings.svg")Extra: Julia sets
For each value \[c\] we can compute the Julia set, namely the set of starting values \[z_1\] for which the iteration over \[z_{n+1}=z_n^2 + c\] converges. Every location on the Mandelbrot image corresponds to its own unique Julia set.
PYTHON
max_iter = 256
center = 0.0+0.0j
extent = 4.0+3.0j
scale = max((extent / width).real, (extent / height).imag)
result = np.zeros((height, width), int)
c = -1.1193+0.2718j
for j in range(height):
for i in range(width):
z = center + (i - width // 2 + (j - height // 2)*1j) * scale
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real > 4.0:
break
result[j, i] = kIf we take the center of the last image, we get the following rendering of the Julia set:
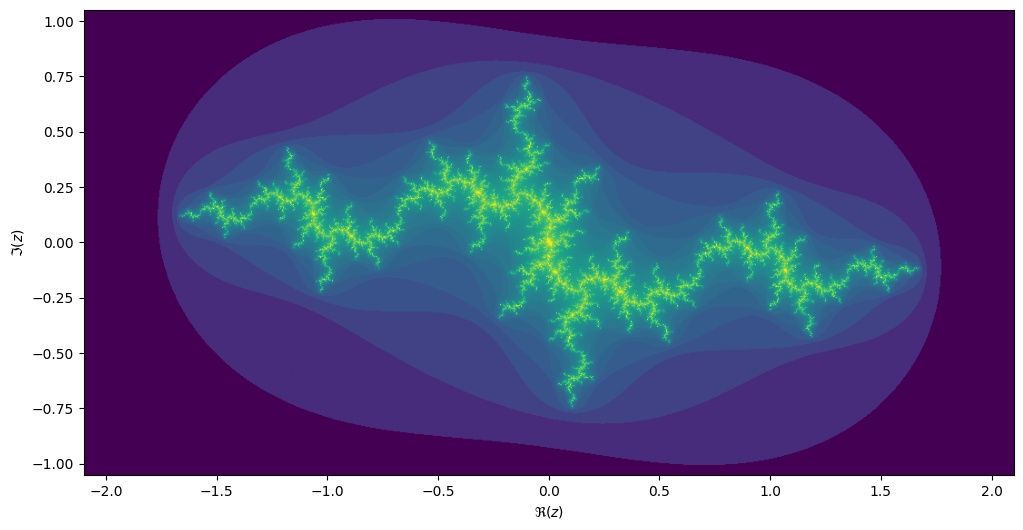
Generalize
Can you generalize your Mandelbrot code, such that you can compute both the Mandelbrot and the Julia sets in an efficient manner, while reusing as much of the code?
Key Points
- Actually making code faster is not always straight forward
- Easy one-liners can get you 80% of the way
- Writing clean, modular code often makes it easier to parallelise later on
Content from Asyncio
Last updated on 2024-09-09 | Edit this page
Overview
Questions
- What is Asyncio?
- When is asyncio usefull?
Objectives
- Understand the difference between a coroutine and a function.
- Know the rudimentary basics of
asyncio. - Perform parallel computations in
asyncio.
Introduction to Asyncio
Asyncio stands for “asynchronous IO”, and as you might have guessed
it has little to do with either asynchronous work or doing IO. In
general, asynchronous is an adjective describing objects or events that
are not coordinated in time. In fact, the asyncio system is
more like a carefully tuned set of gears running a multitude of tasks
as if you have a lot of OS threads running. In the end they are
all powered by the same crank. The gears in asyncio are
called coroutines, its teeth moving other coroutines
wherever you find the await keyword.
The main application for asyncio is hosting back-ends
for web services, where a lot of tasks may be waiting on each other,
while the server still needs to be responsive to new events. In that
respect, asyncio is a little bit outside the domain of
computational science. Nevertheless, you may encounter async code in the
wild, and you can do parallelism with asyncio if
you want a higher level abstraction but don’t want to depend on
dask or a similar alternative.
Many modern programming languages have features that are very similar
to asyncio.
Run-time
The main point of asyncio is that it offers a different
formalism for doing work than what you’re used to from functions. To see
what that means, we need to understand functions a bit better.
Call stacks
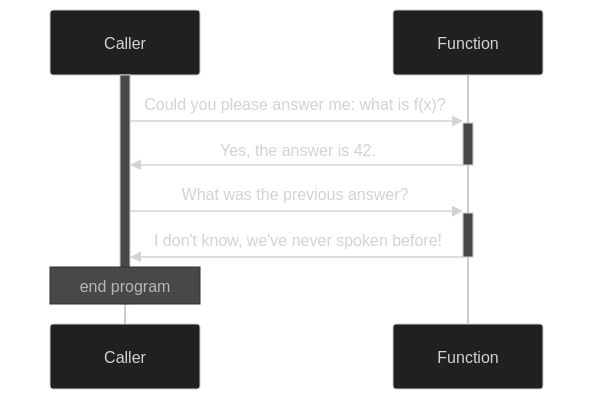
A function call is best understood in terms of a stack based system. When you call a function, you give it its arguments and forget for the moment what you were doing. Or rather, whatever you were doing, push it on a stack and forget about it. Then, with a clean sheet (called a stack frame), you start working on the given arguments until you arrive at a result. This result is what you remember, when you go back to the stack to see what you needed it for in the first place. In this manner, every function call pushes a frame to the stack, and every return statement, we pop back to the previous.
Mermaid code for above diagram
sequenceDiagram
Caller->>+Function: Could you please answer me: what is f(x)?
Function->>-Caller: Yes, the answer is 42.
Caller->>+Function: What was the previous answer?
Function->>-Caller: I don't know, we've never spoken before!Crucially, when we pop back, we forget about the stack frame inside the function. This way, there is always a single concious stream of thought. Function calls can be evaluated by a single active agent.
Coroutines
When working with coroutines, things are a bit different. When a result is returned from a coroutine, the coroutine keeps existing, its context is not forgotten. Coroutines exist in Python in several forms, the simplest being a generator. The following generator produces all integers (if you wait long enough):
Then
or
OUTPUT
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]Mermaid code for above diagram
sequenceDiagram
Caller->>+Integers: Please start counting
Caller-->>Integers: What is the next number?
Integers-->>Caller: 1
Caller-->>Integers: What is the next number?
Integers-->>Caller: 2
GC-->>Integers: I'm sorry, you were forgotten about!
Integers->>-GC: Ok, I'll stop existingChallenge: generate all even numbers
Can you write a generator that generates all even numbers? Try to
reuse integers(). Extra: Can you generate the Fibonacci
numbers?
The generator gives away control, passing a value back, expecting,
maybe, if faith has it, that control will be passed back to it in the
future. The keyword yield applies in all its meanings:
control is yielded, and we have a yield in terms of harvesting a
crop.
A generator conceptually only has one-way traffic: we get output. We
can also use yield the other way around: it can be used to
send information to a coroutine. For instance: we can have a coroutine
that prints whatever you send to it.
PYTHON
def printer():
while True:
x = yield
print(x)
p = printer()
next(p) # we need to advance the coroutine to the first yield
p.send("Mercury")
p.send("Venus")
p.send("Earth")Challenge: line numbers
Change printer to add line numbers to the output.
In practice, the send form of coroutines is hardly ever
used. Cases where you’d need it are rare, and chances are noone will
understand your code. Where it was needed before, its use is now largely
superceded by asyncio.
Now that you have seen coroutines, it is a small step towards
asyncio. The idea is that you can use coroutines to build a
collaborative multi-threading environment. In most modern operating
systems, execution threads are given some time, and then when the OS
needs to do something else, control is taken away pre-emptively. In
collaborative multi-tasking, every worker knows it is
part of a collaborative, and it voluntarily yields control to the
scheduler. With coroutines and yield you should be able to
see that it is possible to create such a system, but it is not so
straight forward, especially when you start to consider the propagation
of exceptions.
Syntax
While asyncio itself is a library in standard Python,
this library is actually a core component for using the associated async
syntax. There are two keywords here: async and
await.
async Is a modifier keyword that modifies the behaviour
of any subsequent syntax to behave in a manner that is consistent with
the asynchronous run-time.
await Is used inside a coroutine to wait for another
coroutine to yield a result. Effectively, control is passed back to the
scheduler, which may decide to give back control when a result is
present.
A first program
Jupyter understands asynchronous code, so you can await
futures in any cell.
PYTHON
import asyncio
async def counter(name):
for i in range(5):
print(f"{name:<10} {i:03}")
await asyncio.sleep(0.2)
await counter("Venus")OUTPUT
Venus 000
Venus 001
Venus 002
Venus 003
Venus 004We can have coroutines work concurrently when we gather
two coroutines.
OUTPUT
Earth 000
Moon 000
Earth 001
Moon 001
Earth 002
Moon 002
Earth 003
Moon 003
Earth 004
Moon 004Note that, although the Earth counter and Moon counter seem to
operate at the same time, in actuality they are alternated by the
scheduler and still running in a single thread! If you work outside the
confines of Jupyter, you need to make sure to create an asynchronous
main function and run it using asyncio.run. A typical
program will look like this:
Asyncio, just like we saw with Dask, is contagious. Once you have
async code at some low level, higher level code also needs to be async:
it’s
turtles all the way down! You may be tempted to do
asyncio.run somewhere from the middle of your normal code
to interact with the asyncronous parts. This can get you into trouble
though, when you get multiple active asyncio run-times. While it is in
principle possible to mix asyncio and classic code, it is in general
considered bad practice to do so.
Timing asynchronous code
While Jupyter works very well with asyncio, one thing
that doesn’t work is line or cell-magic. We’ll have to write our own
timer.
PYTHON
from dataclasses import dataclass
from typing import Optional
from time import perf_counter
from contextlib import asynccontextmanager
@dataclass
class Elapsed:
time: Optional[float] = None
@asynccontextmanager
async def timer():
e = Elapsed()
t = perf_counter()
yield e
e.time = perf_counter() - tNow we can write:
OUTPUT
that took 0.20058414503000677 secondsThese few snippets of code require advanced Python knowledge to
understand. Rest assured that both classic coroutines and
asyncio are a large topic to cover, and we’re not going to
cover all of it. At least, we can now time the execution of our
code!
Compute \(\pi\) again
As a reminder, here is our Numba code to compute \(\pi\).
PYTHON
import random
import numba
@numba.njit(nogil=True)
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / NWe can send work to another thread with
asyncio.to_thread.
Gather multiple outcomes
We’ve seen that we can gather multiple coroutines using
asyncio.gather. Now gather several calc_pi
computations, and time them.
We can put this into a new function calc_pi_split:
PYTHON
async def calc_pi_split(N, M):
lst = await asyncio.gather(*(asyncio.to_thread(calc_pi, N) for _ in range(M)))
return sum(lst) / MNow, see if we get a speed up.
PYTHON
async with timer() as t:
pi = await asyncio.to_thread(calc_pi, 10**8)
print(f"Value of π: {pi}")
print(f"that took {t.time} seconds")OUTPUT
Value of π: 3.1418552
that took 2.3300534340087324 secondsPYTHON
async with timer() as t:
pi = await calc_pi_split(10**7, 10)
print(f"Value of π: {pi}")
print(f"that took {t.time} seconds")OUTPUT
Value of π: 3.1416366400000006
that took 0.5876454019453377 secondsWorking with asyncio outside Jupyter
Jupyter already has an asyncronous loop running for us. If you want
to run scripts outside Jupyter you should write an asynchronous main
function and call it using asyncio.run.
Compute \(\pi\) in a script
Collect what we have done so far to compute \(\pi\) in parallel into a script and run it.
Make sure that you create an async main function, and
run it using asyncio.run. Create a small module called
calc_pi.
Put the Numba code in a separate file
calc_pi/numba.py.
Put the async timer function in a separate file
async_timer.py.
PYTHON
# file: calc_pi/async_pi.py
import asyncio
from async_timer import timer
from .numba import calc_pi
<<async-calc-pi>>
async def main():
calc_pi(1)
<<async-calc-pi-main>>
if __name__ == "__main__":
asyncio.run(main())You may run this using python -m calc_pi.async_pi.
Efficiency
Play with different subdivisions for calc_pi_split such
that M*N remains constant. How much overhead do you
see?
PYTHON
import asyncio
import pandas as pd
from plotnine import ggplot, geom_line, geom_point, aes, scale_y_log10, scale_x_log10
from .numba import calc_pi
from .async_pi import calc_pi_split
from async_timer import timer
calc_pi(1) # compile the numba function
async def main():
timings = []
for njobs in [2**i for i in range(13)]:
jobsize = 2**25 // njobs
print(f"{jobsize} - {njobs}")
async with timer() as t:
await calc_pi_split(jobsize, njobs)
timings.append((jobsize, njobs, t.time))
timings = pd.DataFrame(timings, columns=("jobsize", "njobs", "time"))
plot = ggplot(timings, aes(x="njobs", y="time")) \
+ geom_line() + geom_point() + scale_y_log10() + scale_x_log10()
plot.save("asyncio-timings.svg")
if __name__ == "__main__":
asyncio.run(main())The work takes about 0.1s more when using 1000 tasks, so assuming that overhead scales linearly with the amount of tasks, we can learn that the overhead is around 0.1ms per task.
Key Points
- Use the
asynckeyword to write asynchronous code. - Use
awaitto call coroutines. - Use
asyncio.gatherto collect work. - Use
asyncio.to_threadto perform CPU intensive tasks. - Inside a script: always make an asynchronous
mainfunction, and run it withasyncio.run.
Content from Calling external C and C++ libraries from Python
Last updated on 2023-01-11 | Edit this page
Overview
Questions
- What are some of my options in calling C and C++ libraries from Python code?
- How does this work together with Numpy arrays?
- How do I use this in multiple threads while lifting the GIL?
Objectives
- Compile and link simple C programs into shared libraries.
- Call these library from Python and time its executions.
- Compare the performance with Numba decorated Python code.
- Bypass the GIL when calling these libraries from multiple threads simultaneously.
Calling C and C++ libraries
Simple example using either pybind11 or ctypes
External C and C++ libraries can be called from Python code using a number of options, using e.g. Cython, CFFI, pybind11 and ctypes. We will discuss the last two, because they require the least amount of boilerplate, for simple cases - for more complex examples that may not be the case. Consider this simple C program, test.c, which adds up consecutive numbers:
C
#include <pybind11/pybind11.h>
namespace py = pybind11;
long long sum_range(long long high)
{
long long i;
long long s = 0LL;
for (i = 0LL; i < high; i++)
s += (long long)i;
return s;
}
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "Export the sum_range function as sum_range";
m.def("sum_range", &sum_range, "Adds upp consecutive integer numbers from 0 up to and including high-1");
}You can easily compile and link it into a shared object (.so) file. First you need pybind11. You can install it in a number of ways, like pip, but I prefer creating virtual environments using pipenv.
BASH
pip install pipenv
pipenv install pybind11
pipenv shell
c++ -O3 -Wall -shared -std=c++11 -fPIC `python3 -m pybind11 --includes` test.c -o test_pybind.sowhich generates a test_pybind.so shared object which you
can call from a iPython shell, like this:
PYTHON
%import test_pybind
%sum_range=test_pybind.sum_range
%high=1000000000
%brute_force_sum=sum_range(high)Now you might want to check the output, by comparing with the well-known formula for the sum of consecutive integers. ~~~python %sum_from_formula=high*(high-1)//2 %sum_from_formula %difference=sum_from_formula-brute_force_sum %difference ~~~
Give this script a suitable name, like
call_C_libraries.py. The same thing can be done using
ctypes instead of pybind11, but requires slightly more boilerplate on
the Python side of the code and slightly less on the C side. test.c will
be just the algorithm:
C
long long sum_range(long long high)
{
long long i;
long long s = 0LL;
for (i = 0LL; i < high; i++)
s += (long long)i;
return s;
}Compile and link using ~bash gcc -O3 -g -fPIC -c -o test.o
test.c ld -shared -o libtest.so test.o~
which generates a libtest.so file.
You will need some extra boilerplate:
PYTHON
%import ctypes
%testlib = ctypes.cdll.LoadLibrary("./libtest.so")
%sum_range = testlib.sum_range
%sum_range.argtypes = [ctypes.c_longlong]
%sum_range.restype = ctypes.c_longlong
%high=1000000000
%brute_force_sum=sum_range(high)Again, you can compare with the formula for the sum of consecutive integers. ~~~python %sum_from_formula=high*(high-1)/2 %sum_from_formula %difference=sum_from_formula-brute_force_sum %difference ~~~
Performance
Now we can time our compiled sum_range C library,
e.g. from the iPython interface: ~~~python %timeit sum_range(10**7)
~~~
OUTPUT
2.69 ms ± 6.01 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)If you compare with the Numba timing from chapter 3, you will see that the C library
for sum_range is faster than the numpy computation but
significantly slower than the numba.jit decorated
function.
C versus Numba
Check if the Numba version of this conditional sum range
function outperforms its C counterpart.
Insprired by a blog by Christopher Swenson.
Insert a line if i%3==0: in the code for
sum_range_numba and rename it to
conditional_sum_range_numba.
PYTHON
@numba.jit
def conditional_sum_range_numba(a: int):
x = 0
for i in range(a):
if i%3==0:
x += i
return xLet’s check how fast it runs.
%timeit conditional_sum_range_numba(10**7)OUTPUT
8.11 ms ± 15.6 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Compare this with the run time for the C code for
conditional_sum_range. Compile and link in the usual way, assuming the
file name is still test.c:
Again, we can time our compiled conditional_sum_range C
library, e.g. from the iPython interface:
PYTHON
import ctypes
testlib = ctypes.cdll.LoadLibrary("./libtest.so")
conditional_sum_range = testlib.conditional_sum_range
conditional_sum_range.argtypes = [ctypes.c_longlong]
conditional_sum_range.restype = ctypes.c_longlong
%timeit conditional_sum_range(10**7)OUTPUT
7.62 ms ± 49.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)This shows that for this slightly more complicated example the C code is somewhat faster than the Numba decorated Python code.
Passing Numpy arrays to C libraries.
Now let us consider a more complex example. Instead of computing the
sum of numbers up to a certain upper limit, let us compute that for an
array of upper limits. This will return an array of sums. How difficult
is it to modify our C and Python code to get this done? Well, you just
need to replace &sum_range by
py::vectorize(sum_range):
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", py::vectorize(sum_range), "Adds upp consecutive integer numbers from 0 up to and including high-1");
}Now let’s see what happens if we pass test_pybind.so an
array instead of an integer.
gives
OUTPUT
array([ 0, 0, 1, 3, 6, 10, 15, 21, 28, 36])It does not crash! Instead, it returns an array which you can check to be correct by subtracting the previous sum from each sum (except the first):
which gives
OUTPUT
array([0, 1, 2, 3, 4, 5, 6, 7, 8])the elements of ys - except the last - as you would
expect.
Call the C library from multiple threads simultaneously.
We can quickly show you how the C library compiled using pybind11 can be run multithreaded. try the following from an iPython shell:
OUTPUT
274 ms ± 1.03 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)Now try a straightforward parallellisation of 20 calls of
sum_range, over two threads, so 10 calls per thread. This
should take about 10 * 274ms = 2.74s if parallellisation
were running without overhead. Let’s try:
PYTHON
import threading as T
import time
def timer():
start_time = time.time()
for x in range(10):
t1 = T.Thread(target=sum_range, args=(high,))
t2 = T.Thread(target=sum_range, args=(high,))
t1.start()
t2.start()
t1.join()
t2.join()
end_time = time.time()
print(f"Time elapsed = {end_time-start_time:.2f}s")
timer()This gives
Time elapsed = 5.59si.e. more than twice the time we would expect. What actually happened
is that sum_range was run sequentially instead of
parallelly. We need to add a single declaration to test.c:
py::call_guard<py::gil_scoped_release>():
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", py::vectorize(sum_range), "Adds upp consecutive integer numbers from 0 up to and including high-1");
}like this:
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", &sum_range, "A function which adds upp numbers from 0 up to and including high-1", py::call_guard<py::gil_scoped_release>());
}Now compile again:
BASH
c++ -O3 -Wall -shared -std=c++11 -fPIC `python3 -m pybind11 --includes` test.c -o test_pybind.soReimport the rebuilt shared object - this can only be done by quitting and relaunching the iPython interpreter - and time again.
PYTHON
import test_pybind
import time
import threading as T
sum_range=test_pybind.sum_range
high=int(1e9)
def timer():
start_time = time.time()
for x in range(10):
t1 = T.Thread(target=sum_range, args=(high,))
t2 = T.Thread(target=sum_range, args=(high,))
t1.start()
t2.start()
t1.join()
t2.join()
end_time = time.time()
print(f"Time elapsed = {end_time-start_time:.2f}s")
timer()This gives:
OUTPUT
Time elapsed = 2.81sas you would expect for two sum_range modules running in
parallel.
Key Points
- Multiple options are available in calling external C and C++ libraries and that the best choice can depend on the complexity of your problem.
- Obviously, there is an extra compile and link step, but you will get a much faster execution compared to pure Python.
- Also, the GIL will be circumvented in calling these libaries.
- Numba might also offer you the speedup you want with even less effort.